Array representation of Polynomial. More...
#include <polynomial.hpp>

Public Member Functions | |
| Polynomial () | |
| Default constructor. More... | |
| Polynomial (std::initializer_list< Coeff_t > _list) | |
| List initializer for simple Polynomial construction. More... | |
| template<class InputIt > | |
| Polynomial (InputIt first, InputIt last) | |
| template<size_t N, class Coeff_t2 , class PolyVar2 > | |
| Polynomial (const Polynomial< N, Coeff_t2, PolyVar2 > &poly) | |
| Constructor for constructing higher-order Polynomial types from lower order Polynomial types. More... | |
| Polynomial | operator- () const |
| Unary negative operator to change the sign of a Polynomial. More... | |
Related Functions | |
(Note that these are not member functions.) | |
| template<class Config = DefaultSimplifyConfig, class PolyVar , class ... VarArgs, size_t Order, class Real , typename = typename std::enable_if<Config::expand_to_Polynomial && variable_in<Var<VarArgs...>, PolyVar>::value>::type> | |
| Polynomial< Order+1, Real, PolyVar > | simplify (MultiplyOp< Var< VarArgs... >, Polynomial< Order, Real, PolyVar > > &f) |
| Type trait which determines if an operation (multiplication, addition) can be distributed over the coefficients of a polynomial. More... | |
Polynomial roots | |
| enum | PolyRootBounder |
| Enumeration of the types of root bounding methods we have for solve_real_roots. More... | |
| enum | PolyRootBisector |
| Enumeration of the types of bisection routines we have for solve_real_roots . More... | |
| template<class Coeff_t , size_t Order, class Coeff_t2 , class PolyVar > | |
| Coeff_t | precision (const Polynomial< Order, Coeff_t, PolyVar > &f, const Coeff_t2 &x) |
Calculate a maximum error estimate for the evaluation of the polynomial at 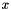 . More... . More... | |
| template<size_t Order, class Coeff_t , class PolyVar > | |
| Polynomial< Order-1, Coeff_t, PolyVar > | deflate_polynomial (const Polynomial< Order, Coeff_t, PolyVar > &a, const double root) |
| Factors out a root of a polynomial and returns a lower-order polynomial with the remaining roots. More... | |
| template<size_t Order, class Coeff_t , class PolyVar > | |
| Polynomial< Order-1, Coeff_t, PolyVar > | deflate_polynomial (const Polynomial< Order, Coeff_t, PolyVar > &a, Null) |
| A specialisation of deflation where the root is at zero. More... | |
| template<class PolyVar > | |
| StackVector< double, 0 > | solve_real_roots (const Polynomial< 0, double, PolyVar > &f) |
| Specialisation for no roots of a 0th order Polynomial. More... | |
| template<class PolyVar > | |
| StackVector< double, 1 > | solve_real_roots (const Polynomial< 1, double, PolyVar > &f) |
| Calculate the single real root (if it exists) of a 1st order Polynomial. More... | |
| template<class PolyVar > | |
| StackVector< double, 2 > | solve_real_roots (Polynomial< 2, double, PolyVar > f) |
| Calcualte the real roots of a 2nd order Polynomial using radicals. More... | |
| template<class PolyVar > | |
| StackVector< double, 3 > | solve_real_roots (const Polynomial< 3, double, PolyVar > &f_original) |
| Calculate the real roots of a 3rd order Polynomial using radicals. More... | |
| template<size_t Order, class Coeff_t , class PolyVar > | |
| detail::SturmChain< Order, Coeff_t, PolyVar > | sturm_chain (const Polynomial< Order, Coeff_t, PolyVar > &f) |
| Helper function to generate a SturmChain from a Polynomial. More... | |
| template<size_t Order, class Coeff_t , class PolyVar > | |
| size_t | descartes_rule_of_signs (const Polynomial< Order, Coeff_t, PolyVar > &f) |
| Calculates an upper bound estimate for the number of positive real roots of a Polynomial (including multiples). More... | |
| template<size_t Order, class Coeff_t , class PolyVar > | |
| size_t | budan_01_test (const Polynomial< Order, Coeff_t, PolyVar > &f) |
Budan's upper bound estimate for the number of real roots in a Polynomial over the range 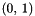 . More... . More... | |
| template<size_t Order, class Coeff_t , class PolyVar > | |
| size_t | alesina_galuzzi_test (const Polynomial< Order, Coeff_t, PolyVar > &f, const Coeff_t &a, const Coeff_t &b) |
Alesina-Galuzzi upper bound estimate for the numer of real roots in a Polynomial over a specified range 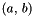 . More... . More... | |
| template<class Coeff_t , size_t Order, class PolyVar > | |
| Coeff_t | LMQ_upper_bound (const Polynomial< Order, Coeff_t, PolyVar > &f) |
| Local-max Quadratic upper bound estimate for the value of the real roots of a Polynomial. More... | |
| template<class Coeff_t , size_t Order, class PolyVar > | |
| Coeff_t | LMQ_lower_bound (const Polynomial< Order, Coeff_t, PolyVar > &f) |
| Local-max Quadratic lower bound estimate for the real roots of a Polynomial. More... | |
| template<class Coeff_t , class PolyVar > | |
| Coeff_t | LMQ_upper_bound (const Polynomial< 0, Coeff_t, PolyVar > &f) |
| Specialisation of Local-max Quadratic upper-bound estimation for real roots of a Polynomial, where the Polynomial is a constant. More... | |
| template<class Coeff_t , class PolyVar > | |
| Coeff_t | LMQ_lower_bound (const Polynomial< 0, Coeff_t, PolyVar > &f) |
| Specialisation of Local-max Quadratic lower-bound estimation for real roots of a Polynomial, where the Polynomial is a constant. More... | |
| template<size_t Order, class Coeff_t , class PolyVar > | |
| StackVector< std::pair< Coeff_t, Coeff_t >, Order > | VCA_real_root_bounds_worker (const Polynomial< Order, Coeff_t, PolyVar > &f) |
Calculate interval bounds on all of the positive real roots between 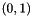 of a squarefree Polynomial. More... of a squarefree Polynomial. More... | |
| template<size_t Order, class Coeff_t , class PolyVar > | |
| StackVector< std::pair< Coeff_t, Coeff_t >, Order > | VCA_real_root_bounds (const Polynomial< Order, Coeff_t, PolyVar > &f) |
| Calculate bounds on all of the positive real roots of a Polynomial. More... | |
| template<size_t Order, class Coeff_t , class PolyVar > | |
| StackVector< std::pair< Coeff_t, Coeff_t >, Order > | VAS_real_root_bounds_worker (Polynomial< Order, Coeff_t, PolyVar > f, MobiusTransform< Coeff_t > M) |
| Calculate bounds on all of the positive real roots in the range of a Polynomial. More... | |
| template<size_t Order, class Coeff_t , class PolyVar > | |
| StackVector< std::pair< Coeff_t, Coeff_t >, Order > | VAS_real_root_bounds (const Polynomial< Order, Coeff_t, PolyVar > &f) |
| Calculate bounds on all of the positive real roots of a Polynomial. More... | |
| template<size_t Order, class Coeff_t , class PolyVar1 , class PolyVar2 = PolyVar1, typename = typename std::enable_if<(Order > 2> | |
| Polynomial< 2, Coeff_t, typename variable_combine< PolyVar1, PolyVar2 >::type > | LinBairstowSolve (Polynomial< Order, Coeff_t, PolyVar1 > f, Coeff_t tolerance, Polynomial< 2, Coeff_t, PolyVar2 > guess={0, 0, 1}) |
| Solve for a quadratic factor of the passed Polynomial using the LinBairstow method. More... | |
| template<class Coeff_t , class PolyVar1 , class PolyVar2 = PolyVar1, size_t Order> | |
| Polynomial< 2, Coeff_t, PolyVar1 > | LinBairstowSolve (Polynomial< Order, Coeff_t, PolyVar1 > f, Coeff_t tolerance, Polynomial< 2, Coeff_t, PolyVar2 > guess={0, 0, 1}) |
| Solve for a quadratic factor of the passed Polynomial using the LinBairstow method. More... | |
| template<class Coeff_t , size_t Order, class PolyVar > | |
| StackVector< Coeff_t, Order > | solve_real_positive_roots_poly_sturm (const Polynomial< Order, Coeff_t, PolyVar > &f, const size_t tol_bits=56) |
| Determine the positive real roots of a polynomial using bisection and Sturm chains. More... | |
| template<PolyRootBounder BoundMode, PolyRootBisector BisectionMode, size_t Order, class Coeff_t , class PolyVar > | |
| StackVector< Coeff_t, Order > | solve_real_positive_roots_poly (const Polynomial< Order, Coeff_t, PolyVar > &f) |
| Iterative solver for the real roots of a square-free Polynomial. More... | |
Polynomial set properties | |
| template<size_t Order, class Coeff_t , class PolyVar > | |
| constexpr Polynomial< Order, Coeff_t, PolyVar > | empty_sum (const Polynomial< Order, Coeff_t, PolyVar > &) |
| Returns the empty sum of a Polynomial. More... | |
Polynomial algebraic operations | |
For all operations below we do not assume that we have a closure. For example, a vector multiplied by a vector is a scalar therefore the * operator may change the returned type of the polynomial. | |
| template<class Coeff_t , size_t Order, class Var1 , class Var2 , class ... VarArgs, typename = typename enable_if_var_in<Var2, Var1>::type> | |
| Polynomial< Order, Coeff_t, Var< VarArgs... > > | sub (const Polynomial< Order, Coeff_t, Var1 > &f, const Relation< Var2, Var< VarArgs... > > &x_container) |
| Optimised Polynomial substitution which performs an exchange of the Polynomial Var. More... | |
| template<size_t Order, class Coeff_t , class PolyVar , class SubVar , typename = typename enable_if_var_in<PolyVar, SubVar>::type> | |
| Coeff_t | sub (const Polynomial< Order, Coeff_t, PolyVar > &f, const Relation< SubVar, Null > &) |
| Optimised Polynomial substitution for Null insertions. More... | |
| template<class Coeff_t , size_t Order, class PolyVar , class SubVar , class Coeff_t2 , typename = typename std::enable_if<!std::is_arithmetic<Coeff_t2>::value || (std::is_base_of<Eigen::EigenBase<Coeff_t2>, Coeff_t2>::value && std::is_arithmetic<Coeff_t2>::value) || (std::is_base_of<Eigen::EigenBase<Coeff_t>, Coeff_t>::value && std::is_arithmetic<Coeff_t2>::value) >::type, typename = typename enable_if_var_in<PolyVar, SubVar>::type> | |
| auto | sub (const Polynomial< Order, Coeff_t, PolyVar > &f, const Relation< SubVar, Coeff_t2 > &x_container) -> STATOR_AUTORETURN(detail::PolySubWorker< Order >::eval(f, x_container._val)) template< size_t D, size_t Order, class Coeff_t, class PolyVar, class Coeff_t2 > std::array< Coeff_t, D+1 > eval_derivatives(const Polynomial< Order, Coeff_t, PolyVar > &f, const Coeff_t2 &x) |
| Symbolically evaluates a Polynomial expression. More... | |
| template<size_t Order1, class Coeff_t , class PolyVar1 , class PolyVar2 , size_t Order2, typename = typename enable_if_var_in<PolyVar1, PolyVar2>::type> | |
| std::tuple< Polynomial< Order1, Coeff_t, typename variable_combine< PolyVar1, PolyVar2 >::type >, Polynomial< Order2 - 1, Coeff_t, typename variable_combine< PolyVar1, PolyVar2 >::type > > | gcd (const Polynomial< Order1, Coeff_t, PolyVar1 > &f, const Polynomial< Order2, Coeff_t, PolyVar2 > &g) |
| Perform Euclidean division of a polynomial. More... | |
| template<size_t Order1, class Coeff_t , class PolyVar1 , class PolyVar2 , typename = typename enable_if_var_in<PolyVar1, PolyVar2>::type> | |
| std::tuple< Polynomial< Order1, Coeff_t, typename variable_combine< PolyVar1, PolyVar2 >::type >, Polynomial< 0, Coeff_t, typename variable_combine< PolyVar1, PolyVar2 >::type > > | gcd (const Polynomial< Order1, Coeff_t, PolyVar1 > &f, const Polynomial< 0, Coeff_t, PolyVar2 > &g) |
| Specialisation for division by a constant. More... | |
Polynomial calculus operations | |
| template<class PolyVar , class ... VarArgs, class Coeff_t , size_t N, typename = typename std::enable_if<(N > 0> | |
| Polynomial< N-1, Coeff_t, typename variable_combine< PolyVar, Var< VarArgs... > >::type > | derivative (const Polynomial< N, Coeff_t, PolyVar > &f, Var< VarArgs... >) |
| Derivatives of Polynomial types. More... | |
| template<class PolyVar , class ... VarArgs, class Coeff_t , size_t N, typename = typename std::enable_if<(N==0) || (!variable_in<PolyVar, Var<VarArgs...> >::value)>::type> | |
| Null | derivative (const Polynomial< N, Coeff_t, PolyVar > &f, Var< VarArgs... >) |
| Derivatives of Polynomial types. More... | |
Polynomial transformations | |
| template<size_t Order, class Coeff_t , class PolyVar > | |
| Polynomial< Order, double, PolyVar > | shift_function (const Polynomial< Order, Coeff_t, PolyVar > &f, const double t) |
Returns a polynomial 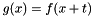 . More... . More... | |
| template<size_t Order, class Coeff_t , class PolyVar > | |
| Polynomial< Order, Coeff_t, PolyVar > | shift_function (const Polynomial< Order, Coeff_t, PolyVar > &f, Unity) |
Returns a polynomial 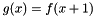 . More... . More... | |
| template<size_t Order, class Coeff_t , class PolyVar > | |
| Polynomial< Order, Coeff_t, PolyVar > | invert_taylor_shift (const Polynomial< Order, Coeff_t, PolyVar > &f) |
Returns a polynomial 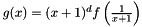 . More... . More... | |
| template<size_t Order, class Coeff_t , class PolyVar > | |
| Polynomial< Order, Coeff_t, PolyVar > | reflect_poly (const Polynomial< Order, Coeff_t, PolyVar > &f) |
Returns a polynomial 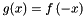 . More... . More... | |
| template<size_t Order, class Coeff_t , class PolyVar > | |
| Polynomial< Order, Coeff_t, PolyVar > | scale_poly (const Polynomial< Order, Coeff_t, PolyVar > &f, const Coeff_t &a) |
Returns a polynomial 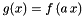 where where 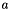 is the scaling factor. More... is the scaling factor. More... | |
Detailed Description
template<size_t Order, class Coeff_t, class PolyVar>
class sym::Polynomial< Order, Coeff_t, PolyVar >
This class allows basic computer algebra to be performed with Polynomial equations.
For example, the polynomial 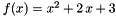 can be created like so:
can be created like so:
And evaluated at the point 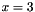 like so:
like so:
The class also functions with Eigen vector or matrix coefficients.
- Template Parameters
-
Order The order of the Polynomial. Coeff_t The type of the coefficients of the Polynomial.
Definition at line 63 of file polynomial.hpp.
Constructor & Destructor Documentation
◆ Polynomial() [1/4]
|
inline |
This initialises all Polynomial orders to be equivalent to zero.
Definition at line 74 of file polynomial.hpp.
◆ Polynomial() [2/4]
|
inline |
This allows a polynomial to be constructed using just a list of coefficients. E.g.
Definition at line 86 of file polynomial.hpp.
◆ Polynomial() [3/4]
|
inline |
Definition at line 99 of file polynomial.hpp.
◆ Polynomial() [4/4]
|
inline |
Definition at line 117 of file polynomial.hpp.
Member Function Documentation
◆ operator-()
|
inline |
Definition at line 126 of file polynomial.hpp.
Friends And Related Function Documentation
◆ alesina_galuzzi_test()
|
related |
This a generalisation of Budan's 01 test (see budan_01_test) and is implemented that way. The polynomial is shifted so that 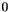 corresponds to
corresponds to 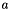 , then scaled so that
, then scaled so that 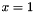 corresponds to
corresponds to 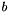 , before Budan's test is called on the transformed Polynomial.
, before Budan's test is called on the transformed Polynomial.
Definition at line 1213 of file polynomial.hpp.
◆ budan_01_test()
|
related |
Budan's test is actually just Descarte's test, but on a transformed Polynomial 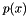 , which is related to
, which is related to 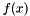 as follows:
as follows:
![\[ p(x) = \left(x+1\right)^d\,f\left(\frac{1}{x+1}\right) \]](form_37.png)
where 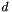 is the order of the polynomial
is the order of the polynomial 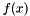 . The roots of
. The roots of 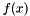 in the range
in the range ![$[0,1]$](form_76.png) are mapped over the range
are mapped over the range ![$[0,\infty]$](form_77.png) of
of 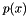 . This allows Descarte's rule of signs to be applied to a limited range of the original polynomial.
. This allows Descarte's rule of signs to be applied to a limited range of the original polynomial.
The actual transformation to 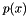 is carried out using the invert_taylor_shift function, before this is passed to descartes_rule_of_signs.
is carried out using the invert_taylor_shift function, before this is passed to descartes_rule_of_signs.
- Returns
- An upper bound on the number of real roots in the interval
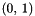 .
.
Definition at line 1198 of file polynomial.hpp.
◆ deflate_polynomial() [1/2]
|
related |
Given a polynomial, we can rearrange it in factored form like so
![\[ \sum_{i=0}^N a_i\,x^i =(x - r_1)\sum_{i=0}^{N-1} b_i\, x^{i} \]](form_45.png)
where 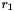 is a root of the polynomial. Equating terms on the LHS with terms on the RHS with equal powers of
is a root of the polynomial. Equating terms on the LHS with terms on the RHS with equal powers of 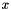 , we have:
, we have:
![\[ b_i=\frac{b_{i-1} - a_i}{r_1}\qquad \textrm{for}\ i\in[1,\,N-1] \]](form_47.png)
This formula, known as backward deflation, can be used to calculate all coefficients using the starting point 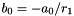 . This approach is not always stable (for example if the root is zero, or if
. This approach is not always stable (for example if the root is zero, or if 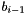 has the same sign as
has the same sign as 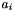 we might have catastrophic cancellation).
we might have catastrophic cancellation).
An alternative "forward" iterative form may be found by substituting 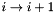 , which gives:
, which gives:
![\[ b_{i} = a_{i+1} + r_1\,b_{i+1} \qquad \textrm{for}\ i\in[0,\,N-2] \]](form_52.png)
Again this approach may be used given the starting point 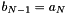 . However, it might also suffer from catastrophic cancellation if
. However, it might also suffer from catastrophic cancellation if 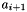 has the opposite sign to
has the opposite sign to 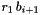 .
.
It should be noted that Numerical Recipies states that "Forward deflation is stable if the largest absolute root is always divided out... backward deflation is stable if the smallest absolute root is always divided out". Unfortunately we do not know a priori the magnitude of the root being divided out.
As both approaches may suffer from catastrophic cancellation, we decide to switch between them. If we catch the special root-is-zero case, we only must avoid catastrophic cancellation. This arises if two non-zero terms are subtracted from each other (i.e., for the first approach this happens if 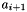 and
and 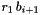 are non-zero and have opposite sign). We could use this to monitor the bits of precision "lost" as we calculate from each end and select a point between the two methods where accuracy is highest, but this would require a more detailed analysis of the error. A simple approach is to solve from both ends of the polynomial at the same time and only actually accept whichever has the lowest catastrophic cancellation accuracy in terms of bits.
are non-zero and have opposite sign). We could use this to monitor the bits of precision "lost" as we calculate from each end and select a point between the two methods where accuracy is highest, but this would require a more detailed analysis of the error. A simple approach is to solve from both ends of the polynomial at the same time and only actually accept whichever has the lowest catastrophic cancellation accuracy in terms of bits.
- Parameters
-
a The Polynomial to factor a root out of. root The root to remove.
Definition at line 660 of file polynomial.hpp.
◆ deflate_polynomial() [2/2]
|
related |
Deflating out a root at zero becomes a division by x. As the constant term is zero, there is no residual and the division becomes a simple shifted copy.
Definition at line 693 of file polynomial.hpp.
◆ derivative() [1/2]
|
related |
This specialisation is only activated if this is a derivative in the correct variable AND the Order of the Polynomial is greater than zero.
Definition at line 402 of file polynomial.hpp.
◆ derivative() [2/2]
|
related |
This specialisation is only activated if this is a derivative in the incorrect variable OR its a low order poly.
Definition at line 417 of file polynomial.hpp.
◆ descartes_rule_of_signs()
|
related |
Descarte's rule of signs states that the number of positive real roots for a single-variable real-coefficient Polynomial is less than or equal to the number of sign changes between consecutive non-zero coefficients in the Polynomial. When the actual root count is less, it is less by an even number. Therefore, the values 0 or 1 are exact.
Definition at line 1161 of file polynomial.hpp.
◆ empty_sum()
|
related |
The empty sum is a term whose multiplicative action is null (can be ignored).
Definition at line 159 of file polynomial.hpp.
◆ gcd() [1/2]
|
related |
Given two polynomials 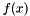 and
and 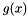 , the Euclidean division is a determination of the quotient polynomial
, the Euclidean division is a determination of the quotient polynomial 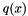 and the remainder polynomial
and the remainder polynomial 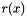 , which satisfy
, which satisfy
![\[ f(x) = g(x)\,q(x) + r(x) \]](form_20.png)
If g(x) only consists of factors of f(x), the remainder will be zero. The algorithm used here is based on polynomial long division.
If the division is by a monomial 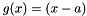 where
where 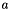 is a root of
is a root of 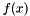 , then the deflate_polynomial function should be used as it is more numerically stable and efficient.
, then the deflate_polynomial function should be used as it is more numerically stable and efficient.
As g(x) may contain leading order coefficients which are zero, we cannot lower the order of the quotient polynomial returned.
Definition at line 340 of file polynomial.hpp.
◆ gcd() [2/2]
|
related |
Definition at line 375 of file polynomial.hpp.
◆ invert_taylor_shift()
|
related |
The creation of 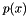 , given by
, given by
![\[ p(x) = \left(x+1\right)^d\,f\left(\frac{1}{x+1}\right) \]](form_37.png)
where 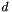 is the order of the polynomial
is the order of the polynomial 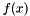 , is often carried out while locating roots of a Polynomial. It has the useful property of generating a polynomial which has the same number of roots of
, is often carried out while locating roots of a Polynomial. It has the useful property of generating a polynomial which has the same number of roots of 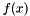 in the range
in the range ![$x\in[0,\,1]$](form_39.png) , but now in the range
, but now in the range ![$x\in[\infty,\,0]$](form_40.png) . Therefore, small sections of a polynomial may be inspected for roots using scaling, shifting, and this transformation. It is a special case of a Mobius transformation of the Polynomial.
. Therefore, small sections of a polynomial may be inspected for roots using scaling, shifting, and this transformation. It is a special case of a Mobius transformation of the Polynomial.
Creation of 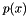 may be carried out in two steps. First, the following equation is generated:
may be carried out in two steps. First, the following equation is generated:
![\[ p_1(x) = x^d\,f\left(\frac{1}{x}\right) \]](form_41.png)
This operation may be performed simply by reversing the order of the coefficient array in the Polynomial. Then, a shift_function is applied to complete the transformation:
![\[ p_2(x) = p_1\left(x+1\right) \]](form_42.png)
This entire operation is performed using an optimised version of the shift_polynomial function. Take a look at the implementation of shift_polynomial and substitute in a shift value of 1 to arrive at this implementation.
Definition at line 530 of file polynomial.hpp.
◆ LinBairstowSolve() [1/2]
|
related |
This function is part of a generic polynomial root finding technique. It returns a quadratic factor of the passed polynomial. The tolerance is the convergence criterion on the coefficients of the factor.
Definition at line 1614 of file polynomial.hpp.
◆ LinBairstowSolve() [2/2]
|
related |
This specialisation is for low-order polynomials, where there is no factorisation to be done and the original
Definition at line 1661 of file polynomial.hpp.
◆ LMQ_lower_bound() [1/2]
|
related |
Given a Polynomial 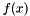 , this function performs the transformation:
, this function performs the transformation:
![\[ g(x) = x^n\,f(\frac{1}{x}) \]](form_82.png)
Now the upper bound on the real roots of 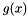 are the inverse of the lower bound on the real roots of
are the inverse of the lower bound on the real roots of 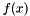 . The transformation is computationally equivalent to reversing the coefficient array of the polynomial
. The transformation is computationally equivalent to reversing the coefficient array of the polynomial 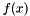 . This function is adapted from the thesis "Upper bounds on the values of the
positive roots of polynomials" by Panagiotis S. Vigklas (2010).
. This function is adapted from the thesis "Upper bounds on the values of the
positive roots of polynomials" by Panagiotis S. Vigklas (2010).
Definition at line 1269 of file polynomial.hpp.
◆ LMQ_lower_bound() [2/2]
|
related |
Definition at line 1289 of file polynomial.hpp.
◆ LMQ_upper_bound() [1/2]
|
related |
This function is adapted from the thesis "Upper bounds on the values of the positive roots of polynomials" by Panagiotis S. Vigklas (2010). The main change is to generalise to arbitrary sign on the highest order coefficient, and to allow high-order coefficients with zero values.
Definition at line 1227 of file polynomial.hpp.
◆ LMQ_upper_bound() [2/2]
|
related |
Definition at line 1279 of file polynomial.hpp.
◆ PolyRootBisector
|
related |
Definition at line 1598 of file polynomial.hpp.
◆ PolyRootBounder
|
related |
Definition at line 1592 of file polynomial.hpp.
◆ precision()
|
related |
The calculation of this value is outlined in "5.6 Root acceptance and refinement" of "A survey of numerical mathematics" vol.1. It is useful for setting accuracy limits while calculating roots.
Definition at line 579 of file polynomial.hpp.
◆ reflect_poly()
|
related |
Definition at line 544 of file polynomial.hpp.
◆ scale_poly()
|
related |
Definition at line 555 of file polynomial.hpp.
◆ shift_function() [1/2]
|
related |
Given a polynomial 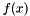 :
:
![\[ f(x) = \sum_{i=0}^N a_i\,x^i \]](form_24.png)
We wish to determine the coefficients of a polynomial 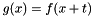 :
:
![\[ g(x) = \sum_{i=0}^N b_i\,x^i \]](form_25.png)
We can define 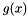 by taking a Taylor expansion of
by taking a Taylor expansion of 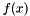 about the point
about the point 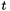 , we have:
, we have:
![\[ g(x) = f(t+x) = \sum_{i=0}^N \frac{f^i(t)}{i!}x^i \]](form_27.png)
where 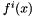 is the
is the 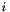 th derivative of
th derivative of 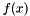 and
and 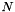 is the order of the polynomial
is the order of the polynomial 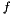 . Each coefficient of
. Each coefficient of 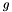 is then given by:
is then given by:
![\[ b_i = \frac{f^i(t)}{i!} \]](form_33.png)
Here, we then use a modified version of the eval_derivatives function to actually calculate the derivatives while avoiding the factorial term.
Definition at line 458 of file polynomial.hpp.
◆ shift_function() [2/2]
|
related |
This is an optimised shift_function operation where the shift is unity. See shift_function for more implementation details.
Definition at line 480 of file polynomial.hpp.
◆ simplify()
|
related |
This general form allows all operations between all constants.
Simplification of a Polynomial LHS multiplied by a Var.
Definition at line 267 of file simplify.hpp.
◆ solve_real_positive_roots_poly()
|
related |
This function assumes that the polynomial has non-zero high and constant coefficients.
Definition at line 1769 of file polynomial.hpp.
◆ solve_real_positive_roots_poly_sturm()
|
related |
Definition at line 1671 of file polynomial.hpp.
◆ solve_real_roots() [1/4]
|
related |
- Parameters
-
f The Polynomial to evaluate.
Definition at line 705 of file polynomial.hpp.
◆ solve_real_roots() [2/4]
|
related |
- Parameters
-
f The Polynomial to evaluate.
Definition at line 715 of file polynomial.hpp.
◆ solve_real_roots() [3/4]
|
related |
Roots are always returned sorted lowest-first.
- Parameters
-
f The Polynomial to evaluate.
Definition at line 730 of file polynomial.hpp.
◆ solve_real_roots() [4/4]
|
related |
Roots are always returned sorted lowest-first.
- Parameters
-
f_original The Polynomial to evaluate.
Definition at line 805 of file polynomial.hpp.
◆ sturm_chain()
|
related |
The actual calculation, storage, and evaluation of the Sturm chain is done by the detail::SturmChain type.
The Sturm chain is a sequence of polynomials 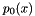 ,
, 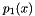 ,
, 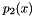 ,
,  ,
, 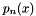 generated from a single polynomial
generated from a single polynomial 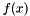 of order
of order 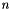 . The first two Sturm chain polynomials are given as
. The first two Sturm chain polynomials are given as
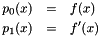
All higher polynomials are evaluated like so:
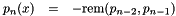
where 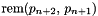 returns the remainder polynomial from a gcd of
returns the remainder polynomial from a gcd of 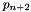 over
over 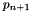 . This sequence terminates at
. This sequence terminates at 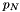 , where
, where 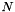 is the order of the original Polynomial,
is the order of the original Polynomial, 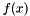 .
.
The interesting property of this chain is that it allows a calculation of the count of distinct real roots of 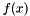 within a certain range. If we evaluate the Sturm chain of
within a certain range. If we evaluate the Sturm chain of 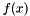 at a point
at a point 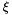 and count the number of changes in sign (ignoring zeros) in the sequence:
and count the number of changes in sign (ignoring zeros) in the sequence:
![\[ p_0(\xi),\,p_1(\xi),\,\ldots p_n(\xi) \]](form_69.png)
and define this as 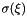 . Then, given two real numbers
. Then, given two real numbers 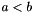 , the number of distinct roots of
, the number of distinct roots of 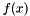 in
in ![$(a,b]$](form_72.png) is given by
is given by 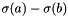 .
.
This gives a method to calculate the exact number of real and distinct roots in a region, which can then be used in a bisection routine to bound individual distinct roots. The Sturm sequence can also be easily evaluated at infinite bounds 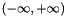 to determine the total number of real roots.
to determine the total number of real roots.
Although this method allows the construction of an arbitrary-order Polynomial root finder through bisection, inexact methods for computing the number of roots in a region (such as descartes_rule_of_signs, used in VAS_real_root_bounds) are preferred as they are more computationally efficient.
Definition at line 1146 of file polynomial.hpp.
◆ sub() [1/3]
|
related |
Definition at line 181 of file polynomial.hpp.
◆ sub() [2/3]
|
related |
Definition at line 188 of file polynomial.hpp.
◆ sub() [3/3]
|
related |
As the intermediate and final return types of a symbolic evaluation are unknown, this must be handled using template metaprogramming to unfold the multiplication. This is provided by the detail::PolySubWorker classes.
The method used to evaluate the polynomial is known as Horner's method.
Definition at line 285 of file polynomial.hpp.
◆ VAS_real_root_bounds()
|
related |
This function uses the VAS algorithm to bound the roots and assumes the polynomial has non-zero constant and leading order coefficients. This function enforces these conditions before passing it to VAS_real_root_bounds_worker.
Definition at line 1569 of file polynomial.hpp.
◆ VAS_real_root_bounds_worker()
|
related |
This function uses the VAS algorithm to bound the roots and assumes the polynomial has non-zero constant and leading order coefficients.
The parameter M is an array of Mobius transformation coefficients {a,b,c,d}. By default it is a direct mapping to the original Polynomial.
Definition at line 1471 of file polynomial.hpp.
◆ VCA_real_root_bounds()
|
related |
This function uses the VCA algorithm to bound the roots and assumes the polynomial has non-zero constant and leading order coefficients. This function enforces these requirements and then simply scales the Polynomial so that all roots lie in the range (0,1) before passing it to VCA_real_root_bounds_worker.
Definition at line 1365 of file polynomial.hpp.
◆ VCA_real_root_bounds_worker()
|
related |
This function uses the VCA algorithm to bound the roots. It assumes that the polynomial has a non-zero constant term and leading order coefficient term.
Definition at line 1302 of file polynomial.hpp.
The documentation for this class was generated from the following files:
- /home/mjki2mb2/stator/stator/symbolic/polynomial.hpp
- /home/mjki2mb2/stator/stator/symbolic/simplify.hpp
 1.8.13
1.8.13