The stator symbolic math library. More...
Namespaces | |
| detail | |
| Namespace containing the details of the implmentation for general stator components. | |
Classes | |
| struct | ApplySymbolicOps |
| Simple combination rule to enable Symbolic operations, but avoid redundantly specifying where two SymbolicOperator classes are operated on. More... | |
| struct | BinaryOp |
| Symbolic representation of a binary symbolic operation. More... | |
| struct | BinaryOp< Expr, Op, Expr > |
| Specialisation of BinaryOp for runtime arguments (Expr). More... | |
| struct | C |
| A class representing a compile-time rational constant (i.e., std::ratio). More... | |
| class | ConstantRT |
| struct | distributive |
| struct | Dynamic |
| Template argument for dynamic types, as well as their base class. More... | |
| struct | enable_if_var_in |
| struct | enable_if_var_not_in |
| struct | expand_Constants |
| struct | expand_Constants_to |
| struct | expand_to_Polynomial |
| struct | Expr |
| The generic holder/smart pointer for a runtime Abstract Syntax Tree (AST) (expression). More... | |
| struct | Factorial |
| Symbolic Factorial function. More... | |
| struct | Factorial< 0 > |
| struct | Factorial< 1 > |
| struct | InvFactorial |
| Symbolic Inverse factorial function. More... | |
| struct | is_C |
| Compile time type-test for compile-time constants C. More... | |
| struct | is_C< C< N, D > > |
| struct | is_whole_factor |
| struct | IsSymbolic |
| struct | left_distributive |
| struct | left_distributive< detail::Multiply, detail::Add > |
| struct | MobiusTransform |
| Class representing the current Mobius transformation applied to a Polynomial. More... | |
| class | Polynomial |
| Array representation of Polynomial. More... | |
| class | Polynomial< Order, C< num, denom >, PolyVar > |
| struct | PowerOpEnableExpansion |
| struct | PowerOpEnableExpansion< Var< VarArgs... > > |
| struct | Relation |
| Symbolic representation of a variable substitution. More... | |
| struct | right_distributive |
| struct | right_distributive< detail::Divide, detail::Add > |
| struct | right_distributive< detail::Power, detail::Multiply > |
| class | RTBase |
| Abstract interface class for all runtime symbolic classes. More... | |
| class | RTBaseHelper |
| CRTP helper base class which implements some of the common boilerplate code for runtime symbolic types. More... | |
| struct | SimplifyConfig |
| struct | SymbolicOperator |
| A type trait to denote symbolic terms (i.e., one that is not yet immediately evaluable to a "normal" type) More... | |
| struct | UnaryOp |
| Symbolic representation of a unary operator (i.e., sin(x)). More... | |
| struct | UnaryOp< Expr, Op > |
| Specialisation of unary operator for runtime arguments and use in runtime expressions (Expr). More... | |
| struct | Var |
| Symbolic representation of a variable. More... | |
| class | Var< Dynamic > |
| Specialisation of Var for runtime variables. More... | |
| struct | variable_combine |
| struct | variable_in |
| struct | vidx |
Typedefs | |
| template<class LHS , class RHS > | |
| using | AddOp = BinaryOp< LHS, detail::Add, RHS > |
| using | DefaultSimplifyConfig = SimplifyConfig<> |
| template<class LHS , class RHS > | |
| using | DivideOp = BinaryOp< LHS, detail::Divide, RHS > |
| typedef detail::C_wrap< stator::constant_ratio::e >::type | e |
A symbolic/compile-time rational approximation of 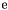 . More... . More... | |
| typedef SimplifyConfig< expand_to_Polynomial, expand_Constants > | ExpandConfig |
| template<class LHS , class RHS > | |
| using | MultiplyOp = BinaryOp< LHS, detail::Multiply, RHS > |
| typedef SimplifyConfig< expand_Constants > | NConfig |
| typedef C< 0 > | Null |
| A symbolic representation of zero. More... | |
| typedef detail::C_wrap< stator::constant_ratio::pi >::type | pi |
A symbolic/compile-time rational approximation of 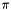 . More... . More... | |
| template<class LHS , class RHS > | |
| using | PowerOp = BinaryOp< LHS, detail::Power, RHS > |
| template<class LHS , class RHS > | |
| using | SubtractOp = BinaryOp< LHS, detail::Subtract, RHS > |
| typedef C< 1 > | Unity |
| A symbolic representation of one. More... | |
| typedef Var< Dynamic > | VarRT |
Enumerations | |
Polynomial roots | |
| enum | PolyRootBounder |
| Enumeration of the types of root bounding methods we have for solve_real_roots. More... | |
| enum | PolyRootBisector |
| Enumeration of the types of bisection routines we have for solve_real_roots . More... | |
Functions | |
| int | abs (int a) |
| long | abs (long a) |
| long long | abs (long long a) |
| float | abs (float a) |
| double | abs (double a) |
| long double | abs (long double a) |
| template<class T > | |
| T | abs (std::complex< T > a) |
| template<class Arg , typename = typename std::enable_if<IsSymbolic<Arg>::value>::type> | |
| auto | abs (const Arg &arg) -> STATOR_AUTORETURN((UnaryOp< decltype(store(arg)), detail::Absolute >(arg))) |
| template<std::intmax_t num, std::intmax_t den> | |
| constexpr C<(1 - 2 *(num< 0)) *num,(1 - 2 *(den< 0)) *den > | abs (const C< num, den > &a) |
| template<class Arg > | |
| auto | arbsign (const Arg &arg) -> STATOR_AUTORETURN((UnaryOp< decltype(store(arg)), detail::Arbsign >(arg))) |
| f _l _r | C< 1 > ())) |
| template<size_t NewOrder, size_t Order, class Coeff_t , class PolyVar > | |
| Polynomial< NewOrder, Coeff_t, PolyVar > | change_order (const Polynomial< Order, Coeff_t, PolyVar > &f) |
| Change the order of a Polynomial. More... | |
| float | cos (float a) |
| double | cos (double a) |
| long double | cos (long double a) |
| template<class T > | |
| std::complex< T > | cos (std::complex< T > a) |
| template<class Arg , typename = typename std::enable_if<IsSymbolic<Arg>::value>::type> | |
| auto | cos (const Arg &arg) -> STATOR_AUTORETURN((UnaryOp< decltype(store(arg)), detail::Cosine >(arg))) |
| template<std::intmax_t num, std::intmax_t den> | |
| auto | cos (const C< num, den > &a) -> STATOR_AUTORETURN(cos_Cimpl(a, detail::select_overload |
| template<std::intmax_t num, std::intmax_t den, typename = typename std::enable_if<is_whole_factor<std::ratio<num, den>, pi>::value>::type> | |
| constexpr Unity | cos_Cimpl (const C< num, den > &a, detail::choice< 0 >) |
| template<std::intmax_t num, std::intmax_t den, typename = typename std::enable_if<is_whole_factor<std::ratio<num, den>, pi, decltype(pi() / C<2>())>::value>::type> | |
| constexpr Null | cos_Cimpl (const C< num, den > &a, detail::choice< 0 >) |
| template<typename Expression > | |
| auto | derivative (const Expression &) |
| Performs a symbolic derivative on the expression. More... | |
| template<class Var , class Arg > | |
| auto | derivative (const UnaryOp< Arg, detail::Sine > &f, Var x) -> STATOR_AUTORETURN(derivative(f._arg, x) *sym::cos(f._arg)) |
| template<class Var , class Arg > | |
| auto | derivative (const UnaryOp< Arg, detail::Cosine > &f, Var x) -> STATOR_AUTORETURN(-derivative(f._arg, x) *sym::sin(f._arg)) |
| template<class Var , class Arg > | |
| auto | derivative (const UnaryOp< Arg, detail::Exp > &f, Var x) -> STATOR_AUTORETURN(derivative(f._arg, x) *f) |
| template<class Var , class Arg > | |
| auto | derivative (const UnaryOp< Arg, detail::Log > &f, Var x) -> STATOR_AUTORETURN(derivative(f._arg, x)/f._arg) |
| template<class Var , class Arg > | |
| auto | derivative (const UnaryOp< Arg, detail::Absolute > &f, Var x) -> STATOR_AUTORETURN(derivative(f._arg, x) *sym::abs(f._arg)/f._arg) |
| template<class Var , class Arg > | |
| auto | derivative (const UnaryOp< Arg, detail::Arbsign > &f, Var x) -> STATOR_AUTORETURN(derivative(f._arg, x) *sym::arbsign(Unity())) |
| template<class T , class ... Args, typename = typename std::enable_if<detail::IsConstant<T>::value>::type> | |
| Null | derivative (const T &, Var< Args... >) |
| Determine the derivative of a symbolic expression. More... | |
| template<class ... Args1, class ... Args2, typename = typename std::enable_if<!std::is_base_of<Dynamic, Var<Args1...> >::value && !std::is_base_of<Dynamic, Var<Args2...> >::value>::type> | |
| auto | derivative (Var< Args1... >, Var< Args2... >) -> typename std::enable_if< Var< Args1... >::idx==Var< Args2... >::idx, Unity >::type |
| Determine the derivative of a variable. More... | |
| template<class ... Args1, class ... Args2, typename = typename std::enable_if<std::is_base_of<Dynamic, Var<Args1...> >::value || std::is_base_of<Dynamic, Var<Args2...> >::value>::type> | |
| Expr | derivative (Var< Args1... > v1, Var< Args2... > v2) |
| Determine the derivative of a variable by another variable. More... | |
| template<class Var > | |
| Expr | derivative (const Expr &f, const Var v) |
| template<class T , typename = typename std::enable_if<std::is_arithmetic<T>::value>::type> | |
| T | empty_sum (const T &) |
| Returns the empty sum of a type. More... | |
| template<class T , typename = typename std::enable_if<std::is_base_of<Eigen::EigenBase<T>, T>::value>::type> | |
| auto | empty_sum (const T &) -> STATOR_AUTORETURN_BYVALUE(T::Zero()) |
| Returns the empty sum of a type. More... | |
| template<class T > | |
| T | empty_sum (const std::complex< T > &) |
| float | exp (float a) |
| double | exp (double a) |
| long double | exp (long double a) |
| template<class T > | |
| std::complex< T > | exp (std::complex< T > a) |
| template<class Arg , typename = typename std::enable_if<IsSymbolic<Arg>::value>::type> | |
| auto | exp (const Arg &arg) -> STATOR_AUTORETURN((UnaryOp< decltype(store(arg)), detail::Exp >(arg))) |
| template<class T > | |
| auto | expand (const T &a) -> STATOR_AUTORETURN(simplify< ExpandConfig >(a)) |
| A variant of simplify that expands into Polynomial types aggressively. More... | |
| template<class Var > | |
| double | fast_sub (const Expr &f, const Relation< Var, double > &rel) |
| template<class T , class Var > | |
| auto | integrate (const T &a, Var) -> typename std::enable_if< std::is_same< decltype(store(derivative(a, Var()))), Null >::value, decltype(store(a *Var()))>::type |
| Integration of any constant/independent expression. More... | |
| template<class ... VarArgs, class LHS , class RHS > | |
| auto | integrate (const AddOp< LHS, RHS > &a, Var< VarArgs... > x) -> STATOR_AUTORETURN(integrate(a._l, x)+integrate(a._r, x)) |
| Distributive integration over addition. More... | |
| template<class ... VarArgs1, class ... VarArgs2, typename = typename enable_if_var_in<Var<VarArgs1...>, Var<VarArgs2...> >::type> | |
| auto | integrate (Var< VarArgs1... >, Var< VarArgs2... >) -> STATOR_AUTORETURN((C< 1, 2 >() *pow< 2 >(typename variable_combine< Var< VarArgs1... >, Var< VarArgs2... > >::type()))) |
| Integration of $x$ by $x$. More... | |
| template<class ... VarArgs1, class ... VarArgs2, std::intmax_t Power, typename = typename enable_if_var_in<Var<VarArgs1...>, Var<VarArgs2...> >::type> | |
| auto | integrate (const PowerOp< Var< VarArgs1... >, C< Power > > &a, Var< VarArgs2... >) -> STATOR_AUTORETURN((C< 1, Power+1 >() *pow(typename variable_combine< Var< VarArgs1... >, Var< VarArgs2... > >::type(), C< Power+1 >()))) |
| Integration of $x^n$ by $x$. More... | |
| template<class T > | |
| constexpr std::enable_if< detail::IsConstant< T >::value, bool >::type | is_constant (const T &) |
| template<class T > | |
| constexpr std::enable_if<!detail::IsConstant< T >::value, bool >::type | is_constant (const T &) |
| bool | is_constant (const Expr &a) |
| float | log (float a) |
| double | log (double a) |
| long double | log (long double a) |
| template<class T > | |
| std::complex< T > | log (std::complex< T > a) |
| template<class Arg , typename = typename std::enable_if<IsSymbolic<Arg>::value>::type> | |
| auto | log (const Arg &arg) -> STATOR_AUTORETURN((UnaryOp< decltype(store(arg)), detail::Log >(arg))) |
| template<class T > | |
| auto | N (const T &a) -> STATOR_AUTORETURN(simplify< NConfig >(a)) |
| A variant of simplify that converts compile time symbols into numbers. More... | |
| template<std::intmax_t n1, std::intmax_t d1, std::intmax_t n2, std::intmax_t d2> | |
| constexpr auto | operator* (C< n1, d1 >, C< n2, d2 >) -> STATOR_AUTORETURN((typename detail::C_wrap< std::ratio_multiply< std::ratio< n1, d1 >, std::ratio< n2, d2 > > >::type())) |
| template<class T , typename = typename std::enable_if<!is_C<T>::value>::type> | |
| Null | operator* (const T &, Null) |
| template<class T , typename = typename std::enable_if<!is_C<T>::value>::type> | |
| Null | operator* (Null, const T &) |
| template<class T , typename = typename std::enable_if<!is_C<T>::value>::type> | |
| auto | operator* (const T &a, Unity) -> STATOR_AUTORETURN(a) |
| template<class T , typename = typename std::enable_if<!is_C<T>::value>::type> | |
| auto | operator* (Unity, const T &a) -> STATOR_AUTORETURN(a) |
| template<std::intmax_t n1, std::intmax_t d1, std::intmax_t n2, std::intmax_t d2> | |
| constexpr auto | operator+ (C< n1, d1 >, C< n2, d2 >) -> STATOR_AUTORETURN((typename detail::C_wrap< std::ratio_add< std::ratio< n1, d1 >, std::ratio< n2, d2 > > >::type())) |
| template<class T , typename = typename std::enable_if<!is_C<T>::value>::type> | |
| T | operator+ (const T &l, Null) |
| template<class T , typename = typename std::enable_if<!is_C<T>::value>::type> | |
| T | operator+ (Null, const T &r) |
| template<std::intmax_t n1, std::intmax_t d1, std::intmax_t n2, std::intmax_t d2> | |
| constexpr auto | operator- (C< n1, d1 >, C< n2, d2 >) -> STATOR_AUTORETURN((typename detail::C_wrap< std::ratio_subtract< std::ratio< n1, d1 >, std::ratio< n2, d2 > > >::type())) |
| template<class T , typename = typename std::enable_if<!is_C<T>::value>::type> | |
| T | operator- (const T &l, Null) |
| template<class T , typename = typename std::enable_if<!is_C<T>::value>::type> | |
| auto | operator- (Null, const T &r) -> STATOR_AUTORETURN(-r) |
| template<std::intmax_t n1, std::intmax_t d1, std::intmax_t n2, std::intmax_t d2> | |
| constexpr auto | operator/ (C< n1, d1 >, C< n2, d2 >) -> STATOR_AUTORETURN((typename detail::C_wrap< std::ratio_divide< std::ratio< n1, d1 >, std::ratio< n2, d2 > > >::type())) |
| template<std::intmax_t Num, std::intmax_t Denom> | |
| std::ostream & | operator<< (std::ostream &os, const C< Num, Denom >) |
| Output operator for compile-time constant (C types). More... | |
| std::ostream & | operator<< (std::ostream &os, const C< 1, 4 >) |
| Output operator specialised for one quarter. More... | |
| std::ostream & | operator<< (std::ostream &os, const C< 1, 2 >) |
| Output operator specialised for one half. More... | |
| std::ostream & | operator<< (std::ostream &os, const C< 3, 4 >) |
| Output operator specialised for three quarters. More... | |
| std::ostream & | operator<< (std::ostream &os, const pi) |
Specialized output operator for 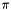 . More... . More... | |
| template<class T > | |
| std::ostream & | operator<< (std::ostream &os, const std::complex< T > &c) |
| template<class T , typename = typename std::enable_if<sym::IsSymbolic<T>::value>::type> | |
| std::ostream & | operator<< (std::ostream &os, const T &v) |
| template<std::intmax_t n1, std::intmax_t d1, std::intmax_t n2, std::intmax_t d2> | |
| constexpr bool | operator== (const C< n1, d1 > &, const C< n2, d2 > &) |
| template<class LHS , class RHS , typename = typename std::enable_if<(std::is_arithmetic<LHS>::value && std::is_arithmetic<RHS>::value)>::type> | |
| auto | pow (const LHS &l, const RHS &r) -> STATOR_AUTORETURN(std::pow(l, r)) |
| template<class LHS , std::intmax_t num, std::intmax_t den, typename = typename std::enable_if<std::is_arithmetic<LHS>::value>::type> | |
| auto | pow (const LHS &l, const C< num, den > &r) -> STATOR_AUTORETURN(std::pow(l, double(r))) |
| template<class LHS , typename = typename std::enable_if<std::is_arithmetic<LHS>::value>::type> | |
| auto | pow (const LHS &l, const C< 1, 3 > &r) -> STATOR_AUTORETURN(std::cbrt(l)) |
| template<class LHS , typename = typename std::enable_if<std::is_arithmetic<LHS>::value>::type> | |
| auto | pow (const LHS &l, const C< 1, 2 > &r) -> STATOR_AUTORETURN(std::sqrt(l)) |
| template<class LHS , typename = typename std::enable_if<std::is_base_of<Eigen::EigenBase<LHS>, LHS>::value>::type> | |
| auto | pow (const LHS &l, const C< 2, 1 > &r) -> STATOR_AUTORETURN_BYVALUE(l.squaredNorm()) |
| template<class LHS > | |
| auto | pow (const LHS &l, const C< 1, 1 > &r) -> STATOR_AUTORETURN(l) |
| template<std::intmax_t num1, std::intmax_t den1, std::intmax_t num2> | |
| auto | pow (const C< num1, den1 > &l, const C< num2, 1 > &r) -> STATOR_AUTORETURN(PowerOpSub< num2 >::eval(sub(l, num2))) |
| template<class F , class Real , typename = typename std::enable_if<detail::IsConstant<F>::value>::type> | |
| double | precision (const F &f, const Real) |
| Estimate the error in evaluating a function at a given time. More... | |
| template<class F , class Real , typename = typename std::enable_if<detail::IsConstant<F>::value>::type> | |
| F | shift_function (const F &f, const Real t) |
Shift a function forward. It returns 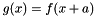 . More... . More... | |
| template<class Config = DefaultSimplifyConfig> | |
| void | simplify () |
| The simplify base implementation. More... | |
| template<class Config = DefaultSimplifyConfig, class Arg , std::intmax_t Power, typename = typename std::enable_if<PowerOpEnableExpansion<Arg>::value>::type> | |
| auto | simplify (const PowerOp< Arg, C< Power, 1 > > &f) -> STATOR_AUTORETURN(simplify_powerop_impl< Config >(f, detail::select_overload |
| Expansion operator for PowerOp types. More... | |
| template<class Config = DefaultSimplifyConfig, class L , class Op , class R > | |
| auto | simplify (BinaryOp< L, Op, R > t) -> STATOR_AUTORETURN(simplify_BinaryOp< Config >(t, detail::select_overload |
| template<class Config = DefaultSimplifyConfig, class PolyVar , class ... VarArgs, size_t Order, class Real , typename = typename std::enable_if<(Config::expand_to_Polynomial && variable_in<Var<VarArgs...>, PolyVar>::value)>::type> | |
| Polynomial< Order+1, Real, typename variable_combine< PolyVar, Var< VarArgs... > >::type > | simplify (const MultiplyOp< Polynomial< Order, Real, PolyVar >, Var< VarArgs... > > &f) |
| Simplification of a Polynomial RHS multiplied by a Var. More... | |
| template<class Config = DefaultSimplifyConfig, class ... VarArgs, typename = typename std::enable_if<Config::expand_to_Polynomial>::type> | |
| auto | simplify (Var< VarArgs... >) -> STATOR_AUTORETURN((Polynomial< 1, int, Var< VarArgs... > > |
| Conversion of a Var to a polynomial if polynomial expansion is enabled. More... | |
| template<class Config = DefaultSimplifyConfig, class ... VarArgs, std::intmax_t Power, typename = typename std::enable_if<Config::expand_to_Polynomial>::type> | |
| Polynomial< Power, int, Var< VarArgs... > > | simplify (const PowerOp< Var< VarArgs... >, C< Power, 1 > > &) |
| Conversion of a PowerOp to a Polynomial when Polynomial expansion is enabled. More... | |
| template<class Config , std::intmax_t num, std::intmax_t den, typename = typename std::enable_if<Config::expand_Constants>::type> | |
| auto | simplify (const C< num, den > &f) -> STATOR_AUTORETURN(typename Config::expand_Constants_to_t(num)/typename Config::expand_Constants_to_t(den)) |
| template<class Config = DefaultSimplifyConfig, class Real1 , size_t N, class Real2 , size_t M, class PolyVar1 , class PolyVar2 , class Op , typename = typename std::enable_if<std::is_same<Op,detail::Add>::value || std::is_same<Op,detail::Subtract>::value>::type, typename = typename enable_if_var_in<PolyVar1, PolyVar2>::type> | |
| auto | simplify (const BinaryOp< Polynomial< N, Real1, PolyVar1 >, Op, Polynomial< M, Real2, PolyVar2 >> &f) -> Polynomial< detail::max_order(M, N), decltype(store(Op::apply(f._l[0], f._r[0]))), typename variable_combine< PolyVar1, PolyVar2 >::type > |
| Addition operator for two Polynomial types. More... | |
| template<class Config = DefaultSimplifyConfig, class Real1 , class Real2 , size_t M, size_t N, class PolyVar1 , class PolyVar2 , class Op , typename = typename std::enable_if<std::is_same<Op,detail::Multiply>::value>::type> | |
| auto | simplify (const BinaryOp< Polynomial< M, Real1, PolyVar1 >, Op, Polynomial< N, Real2, PolyVar2 >> &f) -> Polynomial< M+N, decltype(store(Op::apply(f._l[0], f._r[0]))), typename variable_combine< PolyVar1, PolyVar2 >::type > |
| Multiplication between two Polynomial types. More... | |
| template<class Config = DefaultSimplifyConfig, class Real1 , class Real2 , size_t M, class PolyVar1 , class PolyVar2 > | |
| auto | simplify (const BinaryOp< Polynomial< M, Real1, PolyVar1 >, detail::Divide, Polynomial< 0, Real2, PolyVar2 >> &f) -> Polynomial< M, decltype(store(f._l[0]/f._r[0])), typename variable_combine< PolyVar1, PolyVar2 >::type > |
| Division between two Polynomial types. More... | |
| template<class Config = DefaultSimplifyConfig, class Arg , class Op > | |
| auto | simplify (const UnaryOp< Arg, Op > &f) -> STATOR_AUTORETURN(simplify_UnaryOp< Config >(f, detail::select_overload |
| template<class Config = DefaultSimplifyConfig, class Arg , std::intmax_t Power> | |
| auto | simplify (const PowerOp< UnaryOp< Arg, detail::Arbsign >, C< Power, 1 > > &f) -> typename std::enable_if<!(Power % 2), decltype(try_simplify< Config >(pow(f._l._arg, C< Power >())))>::type |
| Expr | simplify (const Expr &f) |
| template<class Config , class LHS , class RHS , class Op > | |
| auto | simplify_BinaryOp (const BinaryOp< LHS, Op, RHS > &f, detail::choice< 0 >) -> typename std::enable_if<!std::is_same< decltype(Op::apply(f._l, f._r)), BinaryOp< LHS, Op, RHS > >::value, decltype(Op::apply(f._l, f._r))>::type |
| template<class Config , class LHS , class RHS , class Op , typename = typename std::enable_if<std::is_same<RHS, typename Op::right_zero>::value >::type> | |
| Op::right_zero | simplify_BinaryOp (const BinaryOp< LHS, Op, RHS > &, detail::choice< 0 >) |
| template<class Config , class LHS , class RHS , class Op , typename = typename std::enable_if<std::is_same<LHS, typename Op::left_zero>::value && !std::is_same<RHS, typename Op::right_zero>::value>::type> | |
| Op::left_zero | simplify_BinaryOp (const BinaryOp< LHS, Op, RHS > &, detail::choice< 0 >) |
| template<class Config , class LHS , class Op > | |
| auto | simplify_BinaryOp (const BinaryOp< LHS, Op, typename Op::right_identity > &op, detail::choice< 0 >) -> STATOR_AUTORETURN(try_simplify< Config >(op._l)) |
| template<class Config , class RHS , class Op , typename = typename std::enable_if<!std::is_same<RHS, typename Op::right_identity>::value>::type> | |
| auto | simplify_BinaryOp (const BinaryOp< typename Op::left_identity, Op, RHS > &op, detail::choice< 0 >) -> STATOR_AUTORETURN(try_simplify< Config >(op._r)) |
| template<class Config , class ... VarArgs1, class ... VarArgs2, typename = typename enable_if_var_in<Var<VarArgs1...>, Var<VarArgs2...> >::type> | |
| Unity | simplify_BinaryOp (const BinaryOp< Var< VarArgs1... >, detail::Divide, Var< VarArgs2... >> &op, detail::choice< 0 >) |
| template<class Config , class RHS , typename = typename std::enable_if<!std::is_same<RHS, Null>::value>::type> | |
| RHS | simplify_BinaryOp (const SubtractOp< Null, RHS > &r, detail::choice< 0 >) |
| template<class Config , class ... VarArgs1, class ... VarArgs2, typename = typename enable_if_var_in<Var<VarArgs1...>, Var<VarArgs2...> >::type> | |
| auto | simplify_BinaryOp (const MultiplyOp< Var< VarArgs1... >, Var< VarArgs2... > > &, detail::choice< 0 >) -> STATOR_AUTORETURN(sym::pow(typename variable_combine< Var< VarArgs1... >, Var< VarArgs2... > >::type(), C< 2 >())) |
| template<class Config , class ... VarArgs1, class ... VarArgs2, class Order , typename = typename enable_if_var_in<Var<VarArgs1...>, Var<VarArgs2...> >::type> | |
| auto | simplify_BinaryOp (const MultiplyOp< PowerOp< Var< VarArgs1... >, Order >, Var< VarArgs2... > > &f, detail::choice< 0 >) -> STATOR_AUTORETURN(sym::pow(typename variable_combine< Var< VarArgs1... >, Var< VarArgs2... > >::type |
| template<class Config , class ... VarArgs1, class ... VarArgs2, class Order , typename = typename enable_if_var_in<Var<VarArgs1...>, Var<VarArgs2...> >::type> | |
| auto | simplify_BinaryOp (const MultiplyOp< Var< VarArgs1... >, PowerOp< Var< VarArgs2... >, Order > > &f, detail::choice< 0 >) -> STATOR_AUTORETURN(sym::pow(typename variable_combine< Var< VarArgs1... >, Var< VarArgs2... > >::type |
| template<class Config , class LHS , class RHS , class Op > | |
| auto | simplify_BinaryOp (const BinaryOp< LHS, Op, RHS > &f, detail::choice< 2 >) -> STATOR_AUTORETURN(try_simplify< Config >(Op::apply(simplify< Config >(f._l), simplify< Config >(f._r)))) |
| template<class Config , class LHS , class RHS , class Op > | |
| auto | simplify_BinaryOp (const BinaryOp< LHS, Op, RHS > &f, detail::choice< 3 >) -> STATOR_AUTORETURN(try_simplify< Config >(Op::apply(simplify< Config >(f._l), f._r))) |
| template<class Config , class Arg1 , class Arg2 , class Arg3 , class Op , typename = typename std::enable_if<Op::associative>::type> | |
| auto | simplify_BinaryOp (const BinaryOp< BinaryOp< Arg1, Op, Arg2 >, Op, Arg3 > &f, detail::choice< 6 >) -> STATOR_AUTORETURN(try_simplify< Config >(Op::apply(f._l._l, simplify< Config >(BinaryOp< Arg2, Op, Arg3 >(f._l._r, f._r))))) |
| template<class Config , class Arg1 , class Arg2 , class Arg3 , class Op , typename = typename std::enable_if<Op::associative>::type> | |
| auto | simplify_BinaryOp (const BinaryOp< Arg1, Op, BinaryOp< Arg2, Op, Arg3 > > &f, detail::choice< 6 >) -> STATOR_AUTORETURN(try_simplify< Config >(Op::apply(simplify< Config >(BinaryOp< Arg1, Op, Arg2 >(f._l, f._r._l)), f._r._r))) |
| template<class Config , class Arg1 , class Arg2 , class Arg3 , class Op , typename = typename std::enable_if<Op::associative>::type> | |
| auto | simplify_BinaryOp (const BinaryOp< BinaryOp< Arg1, Op, Arg2 >, Op, Arg3 > &f, detail::choice< 7 >) -> STATOR_AUTORETURN(try_simplify< Config >(Op::apply(simplify< Config >(BinaryOp< Arg1, Op, Arg3 >(f._l._l, f._r)), f._l._r))) |
| template<class Config , class Arg1 , class Arg2 , class Arg3 , class Op , typename = typename std::enable_if<Op::associative>::type> | |
| auto | simplify_BinaryOp (const BinaryOp< Arg1, Op, BinaryOp< Arg2, Op, Arg3 > > &f, detail::choice< 7 >) -> STATOR_AUTORETURN(try_simplify< Config >(Op::apply(simplify< Config >(BinaryOp< Arg1, Op, Arg3 >(f._l, f._r._r)), f._r._l))) |
| template<class Config , class PolyVar , size_t Order, class Real , class Op , class Real2 , typename = typename std::enable_if<Config::expand_to_Polynomial && detail::IsConstant<Real2>::value>::type> | |
| auto | simplify_BinaryOp (const BinaryOp< Polynomial< Order, Real, PolyVar >, Op, Real2 > &f, detail::last_choice) -> STATOR_AUTORETURN(try_simplify< Config >(Op::apply(f._l, Polynomial< 0, decltype(toArithmetic(f._r)), PolyVar > |
| Simplification of a Polynomial operating with a constant RHS. More... | |
| template<class Config , class PolyVar , size_t Order, class Real , class Op , class Real2 , typename = typename std::enable_if<Config::expand_to_Polynomial && detail::IsConstant<Real2>::value>::type> | |
| auto | simplify_BinaryOp (const BinaryOp< Real2, Op, Polynomial< Order, Real, PolyVar >> &f, detail::last_choice) -> STATOR_AUTORETURN(try_simplify< Config >(Op::apply(Polynomial< 0, decltype(toArithmetic(f._l)), PolyVar > |
| Simplification of a Polynomial operating with a constant LHS. More... | |
| template<class Config = DefaultSimplifyConfig, class Arg1 , class Arg2 , class Op , typename = typename std::enable_if<std::is_same<Op,detail::Multiply>::value || std::is_same<Op,detail::Divide>::value>::type> | |
| auto | simplify_BinaryOp (const BinaryOp< UnaryOp< Arg1, detail::Arbsign >, Op, UnaryOp< Arg2, detail::Arbsign > > &f, detail::choice< 4 >) -> STATOR_AUTORETURN(try_simplify< Config >(detail::Arbsign::apply(Op::apply(f._l._arg, f._r._arg)))) |
| template<class Config , class LHS , class Arg , class Op , typename = typename std::enable_if<std::is_same<Op,detail::Multiply>::value || std::is_same<Op,detail::Divide>::value>::type> | |
| auto | simplify_BinaryOp (const BinaryOp< LHS, Op, UnaryOp< Arg, detail::Arbsign > > &f, detail::choice< 5 >) -> STATOR_AUTORETURN(try_simplify< Config >(detail::Arbsign::apply(Op::apply(f._l, f._r._arg)))) |
| template<class Config , class RHS , class Arg , class Op , typename = typename std::enable_if<std::is_same<Op,detail::Multiply>::value || std::is_same<Op,detail::Divide>::value>::type> | |
| auto | simplify_BinaryOp (const BinaryOp< UnaryOp< Arg, detail::Arbsign >, Op, RHS > &f, detail::choice< 5 >) -> STATOR_AUTORETURN(try_simplify< Config >(detail::Arbsign::apply(Op::apply(f._l._arg, f._r)))) |
| template<class Config , class Arg , std::intmax_t Power> | |
| auto | simplify_powerop_impl (const PowerOp< Arg, C< Power, 1 > > &f, detail::choice< 0 >) -> STATOR_AUTORETURN(try_simplify< Config >(PowerOpSub< Power >::eval(simplify< Config >(f._l)))) |
| template<class Config , class Arg , std::intmax_t Power> | |
| auto | simplify_powerop_impl (const PowerOp< Arg, C< Power, 1 > > &f, detail::choice< 1 >) -> STATOR_AUTORETURN(simplify< Config >(PowerOpSub< Power >::eval(f._l))) |
| template<class Config , class Arg > | |
| auto | simplify_UnaryOp (const UnaryOp< UnaryOp< Arg, detail::Arbsign >, detail::Arbsign > &f, detail::choice< 0 >) -> STATOR_AUTORETURN(try_simplify< Config >(detail::Arbsign::apply(f._arg._arg))) |
| Specialisation for squares of matrix expressions. More... | |
| template<class Config , class Arg , class Op > | |
| auto | simplify_UnaryOp (const UnaryOp< Arg, Op > &f, detail::last_choice) -> STATOR_AUTORETURN(try_simplify< Config >(Op::apply(simplify< Config >(f._arg)))) |
| float | sin (float a) |
| double | sin (double a) |
| long double | sin (long double a) |
| template<class T > | |
| std::complex< T > | sin (std::complex< T > a) |
| template<class Arg , typename = typename std::enable_if<IsSymbolic<Arg>::value>::type> | |
| auto | sin (const Arg &arg) -> STATOR_AUTORETURN((UnaryOp< decltype(store(arg)), detail::Sine >(arg))) |
| template<std::intmax_t num, std::intmax_t den> | |
| auto | sin (const C< num, den > &a) -> STATOR_AUTORETURN(sin_Cimpl(a, detail::select_overload |
| template<std::intmax_t num, std::intmax_t den, typename = typename std::enable_if<is_whole_factor<std::ratio<num, den>, pi>::value>::type> | |
| constexpr Null | sin_Cimpl (const C< num, den > &a, detail::choice< 0 >) |
| template<std::intmax_t num, std::intmax_t den, typename = typename std::enable_if<is_whole_factor<std::ratio<num, den>, pi, decltype(pi() / C<2>())>::value>::type> | |
| constexpr Unity | sin_Cimpl (const C< num, den > &a, detail::choice< 0 >) |
| StackVector< double, 0 > | solve_real_roots (Null f) |
| template<class LHS , class RHS , class Op , class Var , class Arg > | |
| auto | sub (BinaryOp< LHS, Op, RHS > f, Relation< Var, Arg > x) -> STATOR_AUTORETURN_BYVALUE(Op::apply(sub(f._l, x), sub(f._r, x))) |
| template<class Var , class Arg1 , class Arg2 , class Op > | |
| auto | sub (const UnaryOp< Arg1, Op > &f, const Relation< Var, Arg2 > &x) -> STATOR_AUTORETURN(Op::apply(sub(f._arg, x))) |
| template<class T , class Var , class Arg , typename = typename std::enable_if<detail::IsConstant<T>::value>::type> | |
| auto | sub (const T &f, const Relation< Var, Arg > &) -> STATOR_AUTORETURN_BYVALUE(f) |
| Default implementation of substitution of a symbolic expression at a given point. More... | |
| template<typename ... Args1, typename ... Args2, class Arg , typename = typename enable_if_var_in<Var<Args1...>, Var<Args2...> >::type> | |
| auto | sub (const Var< Args1... > &f, const Relation< Var< Args2... >, Arg > &x) -> STATOR_AUTORETURN_BYVALUE(x._val) |
| Evaluates a symbolic Var at a given point. More... | |
| template<class ... Args1, class Arg , class Var2 , typename = typename enable_if_var_not_in<Var<Args1...>, Var2>::type> | |
| Var< Args1... > | sub (const Var< Args1... > &f, const Relation< Var2, Arg > &x) |
| Evaluates a symbolic Var at a given point. More... | |
| template<class Var , class Arg > | |
| Expr | sub (const Expr &f, const Relation< Var, Arg > &rel) |
| template<size_t Order, class Var , class F , class Real > | |
| auto | taylor_series (const F &f, Real a, Var) -> STATOR_AUTORETURN(try_simplify(detail::TaylorSeriesWorker< 0, Order, Var >::eval(f, a))) |
| Generate a Taylor series representation of a Symbolic expression. More... | |
| template<class T , typename = typename std::enable_if<std::is_arithmetic<T>::value || std::is_base_of<Eigen::EigenBase<T>, T>::value>::type> | |
| auto | toArithmetic (T val) -> STATOR_AUTORETURN_BYVALUE(val) |
| A converter to arithmetic types. More... | |
| template<class T , typename = typename std::enable_if<std::is_arithmetic<T>::value>::type> | |
| auto | toArithmetic (std::complex< T > val) -> STATOR_AUTORETURN_BYVALUE(val) |
| template<std::intmax_t n1, std::intmax_t d1, typename = typename std::enable_if<!(n1 % d1)>::type> | |
| std::intmax_t | toArithmetic (C< n1, d1 > val) |
| template<std::intmax_t n1, std::intmax_t d1, typename = typename std::enable_if<n1 % d1>::type> | |
| double | toArithmetic (C< n1, d1 > val) |
| template<class T > | |
| auto | try_expand (const T &a) -> STATOR_AUTORETURN(try_simplify< ExpandConfig >(a)) |
| A variant of try_simplify that expands into Polynomial types aggressively. More... | |
| template<class T > | |
| auto | try_N (const T &a) -> STATOR_AUTORETURN(try_simplify< NConfig >(a)) |
| A variant of try_simplify that converts compile time symbols into numbers. More... | |
| template<class Config = DefaultSimplifyConfig, class T > | |
| auto | try_simplify (const T &a) -> decltype(detail::try_simplify_imp< Config >(a, detail::select_overload |
| A method to apply simplification only if it is available. More... | |
Symbolic algebra | |
| template<class Arg , typename = typename std::enable_if<IsSymbolic<SymbolicOperator>::value>::type> | |
| Arg | operator+ (const Arg &l) |
| Symbolic unary positive operator. More... | |
| template<class Arg , typename = typename std::enable_if<IsSymbolic<SymbolicOperator>::value>::type> | |
| auto | operator- (const Arg &l) -> STATOR_AUTORETURN(C<-1 >() *l) template< class LHS, class RHS, typename=typename std::enable_if< ApplySymbolicOps< LHS, RHS >::value >::type > auto operator+(const LHS &l, const RHS &r) -> STATOR_AUTORETURN((AddOp< decltype(store(l)), decltype(store(r))>(l, r))) template< class LHS, class RHS, typename=typename std::enable_if< ApplySymbolicOps< LHS, RHS >::value >::type > auto operator*(const LHS &l, const RHS &r) -> STATOR_AUTORETURN((MultiplyOp< decltype(store(l)), decltype(store(r))>(l, r))) template< class LHS, class RHS, typename=typename std::enable_if< ApplySymbolicOps< LHS, RHS >::value >::type > auto operator-(const LHS &l, const RHS &r) -> STATOR_AUTORETURN((SubtractOp< decltype(store(l)), decltype(store(r))>(l, r))) template< class LHS, class RHS, typename=typename std::enable_if< ApplySymbolicOps< LHS, RHS >::value >::type > auto operator/(const LHS &l, const RHS &r) -> STATOR_AUTORETURN((DivideOp< decltype(store(l)), decltype(store(r))>(l, r))) template< class LHS, class RHS, typename=typename std::enable_if< ApplySymbolicOps< LHS, RHS >::value >::type > auto pow(const LHS &l, const RHS &r) -> STATOR_AUTORETURN((PowerOp< decltype(store(l)), decltype(store(r))>(l, r))) |
| Symbolic unary negation operator. More... | |
| template<class Var , class LHS , class RHS > | |
| auto | derivative (const AddOp< LHS, RHS > &f, Var v) -> STATOR_AUTORETURN(derivative(f._l, v)+derivative(f._r, v)) template< class Var, class LHS, class RHS > auto derivative(const SubtractOp< LHS, RHS > &f, Var v) -> STATOR_AUTORETURN(derivative(f._l, v) - derivative(f._r, v)) template< class Var, class LHS, class RHS > auto derivative(const MultiplyOp< LHS, RHS > &f, Var v) -> STATOR_AUTORETURN(derivative(f._l, v) *f._r+f._l *derivative(f._r, v)) template< class Var, class LHS, class RHS > auto derivative(const DivideOp< LHS, RHS > &f, Var v) -> STATOR_AUTORETURN((derivative(f._l, v) *f._r - f._l *derivative(f._r, v))/pow(f._r, C< 2 >())) template< class Var, class Arg, std::intmax_t num, std::intmax_t den > auto derivative(const PowerOp< Arg, C< num, den > > &f, Var v) -> STATOR_AUTORETURN((C< num, den >() *derivative(f._l, v) *pow(f._l, C< num, den >() -C< 1 >()))) |
| Derivatives of AddOp operations. More... | |
| template<class Var , class Arg , class Power > | |
| auto | derivative (const PowerOp< Arg, Power > &f, Var v) -> STATOR_AUTORETURN(f._r *derivative(f._l, v) *pow(f._l, f._r - C< 1 >())+derivative(f._r, v) *log(f._l) *f) |
| Derivative of a PowerOp operation. More... | |
Math functions | |
| template<class T > | |
| size_t | subtraction_precision (const T f1, const T f2) |
| Calculate a "precision" for subtraction between two float types. More... | |
| template<class T > | |
| size_t | addition_precision (const T f1, const T f2) |
| Calculate a "precision" for addition between two float types. More... | |
Variables | |
| f | _r |
Detailed Description
This namespace encapsulates the symbolic math functionality of stator. This library allows you to perform compile-time operations on mathematical expressions, as well as perform run-time calculations, such as root finding on polynomials.
Typedef Documentation
◆ AddOp
| using sym::AddOp = typedef BinaryOp<LHS, detail::Add, RHS> |
Definition at line 180 of file binary_ops.hpp.
◆ DefaultSimplifyConfig
| using sym::DefaultSimplifyConfig = typedef SimplifyConfig<> |
Definition at line 59 of file simplify.hpp.
◆ DivideOp
| using sym::DivideOp = typedef BinaryOp<LHS, detail::Divide, RHS> |
Definition at line 183 of file binary_ops.hpp.
◆ e
| typedef detail::C_wrap<stator::constant_ratio::e>::type sym::e |
Definition at line 59 of file constants.hpp.
◆ ExpandConfig
Definition at line 84 of file simplify.hpp.
◆ MultiplyOp
| using sym::MultiplyOp = typedef BinaryOp<LHS, detail::Multiply, RHS> |
Definition at line 182 of file binary_ops.hpp.
◆ NConfig
| typedef SimplifyConfig<expand_Constants> sym::NConfig |
Definition at line 104 of file simplify.hpp.
◆ Null
Definition at line 51 of file constants.hpp.
◆ pi
| typedef detail::C_wrap<stator::constant_ratio::pi>::type sym::pi |
Definition at line 56 of file constants.hpp.
◆ PowerOp
| using sym::PowerOp = typedef BinaryOp<LHS, detail::Power, RHS> |
Definition at line 184 of file binary_ops.hpp.
◆ SubtractOp
| using sym::SubtractOp = typedef BinaryOp<LHS, detail::Subtract, RHS> |
Definition at line 181 of file binary_ops.hpp.
◆ Unity
| typedef C<1> sym::Unity |
Definition at line 53 of file constants.hpp.
◆ VarRT
| typedef Var<Dynamic> sym::VarRT |
Definition at line 58 of file runtime.hpp.
Enumeration Type Documentation
◆ PolyRootBisector
|
related |
Definition at line 1598 of file polynomial.hpp.
◆ PolyRootBounder
|
related |
Definition at line 1592 of file polynomial.hpp.
Function Documentation
◆ abs() [1/9]
|
inline |
Definition at line 55 of file unary_ops.hpp.
◆ abs() [2/9]
|
inline |
Definition at line 56 of file unary_ops.hpp.
◆ abs() [3/9]
|
inline |
Definition at line 57 of file unary_ops.hpp.
◆ abs() [4/9]
|
inline |
Definition at line 58 of file unary_ops.hpp.
◆ abs() [5/9]
|
inline |
Definition at line 59 of file unary_ops.hpp.
◆ abs() [6/9]
|
inline |
Definition at line 60 of file unary_ops.hpp.
◆ abs() [7/9]
| T sym::abs | ( | std::complex< T > | a | ) |
Definition at line 61 of file unary_ops.hpp.
◆ abs() [8/9]
| auto sym::abs | ( | const Arg & | arg | ) | -> STATOR_AUTORETURN((UnaryOp< decltype(store(arg)), detail::Absolute >(arg))) |
◆ abs() [9/9]
| constexpr C<(1 - 2 * (num < 0)) * num, (1 - 2 * (den < 0)) * den> sym::abs | ( | const C< num, den > & | a | ) |
Definition at line 189 of file constants.hpp.
◆ addition_precision()
| size_t sym::addition_precision | ( | const T | f1, |
| const T | f2 | ||
| ) |
See subtraction_precision.
This function also handles the special cases where one or more of the arguments.
Definition at line 69 of file precision.hpp.
◆ arbsign()
| auto sym::arbsign | ( | const Arg & | arg | ) | -> STATOR_AUTORETURN((UnaryOp< decltype(store(arg)), detail::Arbsign >(arg))) |
◆ C< 1 >()
◆ change_order()
| Polynomial<NewOrder, Coeff_t, PolyVar> sym::change_order | ( | const Polynomial< Order, Coeff_t, PolyVar > & | f | ) |
This can be dangerous, as if the order of a polynomial is lowered high order terms are simply truncated.
Definition at line 140 of file polynomial.hpp.
◆ cos() [1/6]
|
inline |
Definition at line 40 of file unary_ops.hpp.
◆ cos() [2/6]
|
inline |
Definition at line 41 of file unary_ops.hpp.
◆ cos() [3/6]
|
inline |
Definition at line 42 of file unary_ops.hpp.
◆ cos() [4/6]
| std::complex<T> sym::cos | ( | std::complex< T > | a | ) |
Definition at line 43 of file unary_ops.hpp.
◆ cos() [5/6]
| auto sym::cos | ( | const Arg & | arg | ) | -> STATOR_AUTORETURN((UnaryOp< decltype(store(arg)), detail::Cosine >(arg))) |
◆ cos() [6/6]
| auto sym::cos | ( | const C< num, den > & | a | ) | -> STATOR_AUTORETURN(cos_Cimpl(a, detail::select_overload |
Definition at line 186 of file constants.hpp.
◆ cos_Cimpl() [1/2]
| constexpr Unity sym::cos_Cimpl | ( | const C< num, den > & | a, |
| detail::choice< 0 > | |||
| ) |
Definition at line 176 of file constants.hpp.
◆ cos_Cimpl() [2/2]
| constexpr Null sym::cos_Cimpl | ( | const C< num, den > & | a, |
| detail::choice< 0 > | |||
| ) |
Definition at line 180 of file constants.hpp.
◆ derivative() [1/13]
| auto sym::derivative | ( | const Expression & | ) |
◆ derivative() [2/13]
| auto sym::derivative | ( | const UnaryOp< Arg, detail::Sine > & | f, |
| Var | x | ||
| ) | -> STATOR_AUTORETURN(derivative(f._arg, x) *sym::cos(f._arg)) |
◆ derivative() [3/13]
| auto sym::derivative | ( | const UnaryOp< Arg, detail::Cosine > & | f, |
| Var | x | ||
| ) | -> STATOR_AUTORETURN(-derivative(f._arg, x) *sym::sin(f._arg)) |
◆ derivative() [4/13]
| auto sym::derivative | ( | const UnaryOp< Arg, detail::Exp > & | f, |
| Var | x | ||
| ) | -> STATOR_AUTORETURN(derivative(f._arg, x) *f) |
◆ derivative() [5/13]
| auto sym::derivative | ( | const UnaryOp< Arg, detail::Log > & | f, |
| Var | x | ||
| ) | -> STATOR_AUTORETURN(derivative(f._arg, x)/f._arg) |
◆ derivative() [6/13]
| auto sym::derivative | ( | const UnaryOp< Arg, detail::Absolute > & | f, |
| Var | x | ||
| ) | -> STATOR_AUTORETURN(derivative(f._arg, x) *sym::abs(f._arg)/f._arg) |
◆ derivative() [7/13]
| auto sym::derivative | ( | const UnaryOp< Arg, detail::Arbsign > & | f, |
| Var | x | ||
| ) | -> STATOR_AUTORETURN(derivative(f._arg, x) *sym::arbsign(Unity())) |
◆ derivative() [8/13]
| Null sym::derivative | ( | const T & | , |
| Var< Args... > | |||
| ) |
This default implementation gives all consants derivative of zero.
Definition at line 204 of file symbolic.hpp.
◆ derivative() [9/13]
| auto sym::derivative | ( | Var< Args1... > | , |
| Var< Args2... > | |||
| ) | -> typename std::enable_if<Var<Args1...>::idx == Var<Args2...>::idx, Unity>::type |
Determine the derivative of a variable by another variable.
If the variable is the variable in which a derivative is being taken, then this overload should be selected to return Unity.
If the variable is NOT the variable in which a derivative is being taken, then this overload should be selected to return Null.
Definition at line 214 of file symbolic.hpp.
◆ derivative() [10/13]
| Expr sym::derivative | ( | Var< Args1... > | v1, |
| Var< Args2... > | v2 | ||
| ) |
If the variable is NOT the variable in which a derivative is being taken, then this overload should be selected to return Null.
Definition at line 234 of file runtime.hpp.
◆ derivative() [11/13]
| auto sym::derivative | ( | const AddOp< LHS, RHS > & | f, |
| Var | v | ||
| ) | -> STATOR_AUTORETURN(derivative(f._l, v)+derivative(f._r, v)) template< class Var, class LHS, class RHS > auto derivative(const SubtractOp< LHS, RHS > &f, Var v) -> STATOR_AUTORETURN(derivative(f._l, v) - derivative(f._r, v)) template< class Var, class LHS, class RHS > auto derivative(const MultiplyOp< LHS, RHS > &f, Var v) -> STATOR_AUTORETURN(derivative(f._l, v) *f._r+f._l *derivative(f._r, v)) template< class Var, class LHS, class RHS > auto derivative(const DivideOp< LHS, RHS > &f, Var v) -> STATOR_AUTORETURN((derivative(f._l, v) *f._r - f._l *derivative(f._r, v))/pow(f._r, C< 2 >())) template< class Var, class Arg, std::intmax_t num, std::intmax_t den > auto derivative(const PowerOp< Arg, C< num, den > > &f, Var v) -> STATOR_AUTORETURN((C< num, den >() *derivative(f._l, v) *pow(f._l, C< num, den >() -C< 1 >()))) |
◆ derivative() [12/13]
| auto sym::derivative | ( | const PowerOp< Arg, Power > & | f, |
| Var | v | ||
| ) | -> STATOR_AUTORETURN(f._r *derivative(f._l, v) *pow(f._l, f._r - C< 1 >())+derivative(f._r, v) *log(f._l) *f) |
◆ derivative() [13/13]
Definition at line 618 of file runtime.hpp.
◆ empty_sum() [1/3]
| T sym::empty_sum | ( | const T & | ) |
The empty sum is a term whose additive (and typically its subtractive) action is null (can be ignored). This definition only applies for selected types and assumes that their default constructors create the empty sum.
Definition at line 153 of file symbolic.hpp.
◆ empty_sum() [2/3]
| auto sym::empty_sum | ( | const T & | ) |
The empty sum is a term whose additive (and typically its subtractive) action is null (can be ignored). This definition only applies for selected types and assumes that their default constructors create the empty sum.
Definition at line 153 of file symbolic.hpp.
◆ empty_sum() [3/3]
| T sym::empty_sum | ( | const std::complex< T > & | ) |
Definition at line 159 of file symbolic.hpp.
◆ exp() [1/5]
|
inline |
Definition at line 45 of file unary_ops.hpp.
◆ exp() [2/5]
|
inline |
Definition at line 46 of file unary_ops.hpp.
◆ exp() [3/5]
|
inline |
Definition at line 47 of file unary_ops.hpp.
◆ exp() [4/5]
| std::complex<T> sym::exp | ( | std::complex< T > | a | ) |
Definition at line 48 of file unary_ops.hpp.
◆ exp() [5/5]
| auto sym::exp | ( | const Arg & | arg | ) | -> STATOR_AUTORETURN((UnaryOp< decltype(store(arg)), detail::Exp >(arg))) |
◆ expand()
| auto sym::expand | ( | const T & | a | ) | -> STATOR_AUTORETURN(simplify< ExpandConfig >(a)) |
◆ fast_sub()
Definition at line 702 of file runtime.hpp.
◆ integrate() [1/4]
| auto sym::integrate | ( | const T & | a, |
| Var | |||
| ) | -> typename std::enable_if<std::is_same<decltype(store(derivative( a , Var ()))), Null>::value, decltype(store(a * Var()))>::type |
We test if an expression is independant by checking that its derivative is nullary zero.
Definition at line 39 of file integrate.hpp.
◆ integrate() [2/4]
| auto sym::integrate | ( | const AddOp< LHS, RHS > & | a, |
| Var< VarArgs... > | x | ||
| ) | -> STATOR_AUTORETURN(integrate(a._l, x) + integrate(a._r, x)) |
distribute integration through RHS constant multiplication.
distribute integration through LHS constant multiplication.
Distributive integration over subtraction.
Definition at line 55 of file integrate.hpp.
◆ integrate() [3/4]
| auto sym::integrate | ( | Var< VarArgs1... > | , |
| Var< VarArgs2... > | |||
| ) | -> STATOR_AUTORETURN((C< 1, 2 >() *pow< 2 >(typename variable_combine< Var< VarArgs1... >, Var< VarArgs2... > >::type()))) |
◆ integrate() [4/4]
| auto sym::integrate | ( | const PowerOp< Var< VarArgs1... >, C< Power > > & | a, |
| Var< VarArgs2... > | |||
| ) | -> STATOR_AUTORETURN((C< 1, Power+1 >() *pow(typename variable_combine< Var< VarArgs1... >, Var< VarArgs2... > >::type(), C< Power+1 >()))) |
◆ is_constant() [1/3]
| constexpr std::enable_if<detail::IsConstant<T>::value, bool>::type sym::is_constant | ( | const T & | ) |
Definition at line 140 of file symbolic.hpp.
◆ is_constant() [2/3]
| constexpr std::enable_if<!detail::IsConstant<T>::value, bool>::type sym::is_constant | ( | const T & | ) |
Definition at line 143 of file symbolic.hpp.
◆ is_constant() [3/3]
| bool sym::is_constant | ( | const Expr & | a | ) |
Definition at line 651 of file runtime.hpp.
◆ log() [1/5]
|
inline |
Definition at line 50 of file unary_ops.hpp.
◆ log() [2/5]
|
inline |
Definition at line 51 of file unary_ops.hpp.
◆ log() [3/5]
|
inline |
Definition at line 52 of file unary_ops.hpp.
◆ log() [4/5]
| std::complex<T> sym::log | ( | std::complex< T > | a | ) |
Definition at line 53 of file unary_ops.hpp.
◆ log() [5/5]
| auto sym::log | ( | const Arg & | arg | ) | -> STATOR_AUTORETURN((UnaryOp< decltype(store(arg)), detail::Log >(arg))) |
◆ N()
| auto sym::N | ( | const T & | a | ) | -> STATOR_AUTORETURN(simplify< NConfig >(a)) |
◆ operator*() [1/5]
| constexpr auto sym::operator* | ( | C< n1, d1 > | , |
| C< n2, d2 > | |||
| ) | -> STATOR_AUTORETURN((typename detail::C_wrap< std::ratio_multiply< std::ratio< n1, d1 >, std::ratio< n2, d2 > > >::type())) |
◆ operator*() [2/5]
| Null sym::operator* | ( | const T & | , |
| Null | |||
| ) |
Definition at line 133 of file constants.hpp.
◆ operator*() [3/5]
| Null sym::operator* | ( | Null | , |
| const T & | |||
| ) |
Definition at line 135 of file constants.hpp.
◆ operator*() [4/5]
| auto sym::operator* | ( | const T & | a, |
| Unity | |||
| ) | -> STATOR_AUTORETURN(a) |
◆ operator*() [5/5]
| auto sym::operator* | ( | Unity | , |
| const T & | a | ||
| ) | -> STATOR_AUTORETURN(a) |
◆ operator+() [1/4]
| constexpr auto sym::operator+ | ( | C< n1, d1 > | , |
| C< n2, d2 > | |||
| ) | -> STATOR_AUTORETURN((typename detail::C_wrap< std::ratio_add< std::ratio< n1, d1 >, std::ratio< n2, d2 > > >::type())) |
◆ operator+() [2/4]
| T sym::operator+ | ( | const T & | l, |
| Null | |||
| ) |
Definition at line 125 of file constants.hpp.
◆ operator+() [3/4]
| T sym::operator+ | ( | Null | , |
| const T & | r | ||
| ) |
Definition at line 127 of file constants.hpp.
◆ operator+() [4/4]
| Arg sym::operator+ | ( | const Arg & | l | ) |
Definition at line 215 of file binary_ops.hpp.
◆ operator-() [1/4]
| constexpr auto sym::operator- | ( | C< n1, d1 > | , |
| C< n2, d2 > | |||
| ) | -> STATOR_AUTORETURN((typename detail::C_wrap< std::ratio_subtract< std::ratio< n1, d1 >, std::ratio< n2, d2 > > >::type())) |
◆ operator-() [2/4]
| T sym::operator- | ( | const T & | l, |
| Null | |||
| ) |
Definition at line 129 of file constants.hpp.
◆ operator-() [3/4]
| auto sym::operator- | ( | Null | , |
| const T & | r | ||
| ) | -> STATOR_AUTORETURN(-r) |
◆ operator-() [4/4]
| auto sym::operator- | ( | const Arg & | l | ) | -> STATOR_AUTORETURN(C<-1 >() *l) template< class LHS, class RHS, typename=typename std::enable_if< ApplySymbolicOps< LHS, RHS >::value >::type > auto operator+(const LHS &l, const RHS &r) -> STATOR_AUTORETURN((AddOp< decltype(store(l)), decltype(store(r))>(l, r))) template< class LHS, class RHS, typename=typename std::enable_if< ApplySymbolicOps< LHS, RHS >::value >::type > auto operator*(const LHS &l, const RHS &r) -> STATOR_AUTORETURN((MultiplyOp< decltype(store(l)), decltype(store(r))>(l, r))) template< class LHS, class RHS, typename=typename std::enable_if< ApplySymbolicOps< LHS, RHS >::value >::type > auto operator-(const LHS &l, const RHS &r) -> STATOR_AUTORETURN((SubtractOp< decltype(store(l)), decltype(store(r))>(l, r))) template< class LHS, class RHS, typename=typename std::enable_if< ApplySymbolicOps< LHS, RHS >::value >::type > auto operator/(const LHS &l, const RHS &r) -> STATOR_AUTORETURN((DivideOp< decltype(store(l)), decltype(store(r))>(l, r))) template< class LHS, class RHS, typename=typename std::enable_if< ApplySymbolicOps< LHS, RHS >::value >::type > auto pow(const LHS &l, const RHS &r) -> STATOR_AUTORETURN((PowerOp< decltype(store(l)), decltype(store(r))>(l, r))) |
◆ operator/()
| constexpr auto sym::operator/ | ( | C< n1, d1 > | , |
| C< n2, d2 > | |||
| ) | -> STATOR_AUTORETURN((typename detail::C_wrap< std::ratio_divide< std::ratio< n1, d1 >, std::ratio< n2, d2 > > >::type())) |
◆ operator<<() [1/7]
|
inline |
Definition at line 63 of file constants.hpp.
◆ operator<<() [2/7]
|
inline |
Definition at line 71 of file constants.hpp.
◆ operator<<() [3/7]
|
inline |
Definition at line 77 of file constants.hpp.
◆ operator<<() [4/7]
|
inline |
Definition at line 82 of file constants.hpp.
◆ operator<<() [5/7]
|
inline |
Specialized output operator for 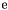 .
.
Definition at line 87 of file constants.hpp.
◆ operator<<() [6/7]
|
inline |
Definition at line 152 of file constants.hpp.
◆ operator<<() [7/7]
| std::ostream& sym::operator<< | ( | std::ostream & | os, |
| const T & | v | ||
| ) |
◆ operator==()
| constexpr bool sym::operator== | ( | const C< n1, d1 > & | , |
| const C< n2, d2 > & | |||
| ) |
Definition at line 121 of file constants.hpp.
◆ pow() [1/7]
| auto sym::pow | ( | const LHS & | l, |
| const RHS & | r | ||
| ) | -> STATOR_AUTORETURN(std::pow(l, r)) |
◆ pow() [2/7]
| auto sym::pow | ( | const LHS & | l, |
| const C< num, den > & | r | ||
| ) | -> STATOR_AUTORETURN(std::pow(l, double(r))) |
◆ pow() [3/7]
| auto sym::pow | ( | const LHS & | l, |
| const C< 1, 3 > & | r | ||
| ) | -> STATOR_AUTORETURN(std::cbrt(l)) |
◆ pow() [4/7]
| auto sym::pow | ( | const LHS & | l, |
| const C< 1, 2 > & | r | ||
| ) | -> STATOR_AUTORETURN(std::sqrt(l)) |
◆ pow() [5/7]
| auto sym::pow | ( | const LHS & | l, |
| const C< 2, 1 > & | r | ||
| ) | -> STATOR_AUTORETURN_BYVALUE(l.squaredNorm()) |
◆ pow() [6/7]
| auto sym::pow | ( | const LHS & | l, |
| const C< 1, 1 > & | r | ||
| ) | -> STATOR_AUTORETURN(l) |
◆ pow() [7/7]
| auto sym::pow | ( | const C< num1, den1 > & | l, |
| const C< num2, 1 > & | r | ||
| ) | -> STATOR_AUTORETURN(PowerOpSub< num2 >::eval(sub(l, num2))) |
◆ precision()
|
inline |
Definition at line 247 of file symbolic.hpp.
◆ shift_function()
|
inline |
For constant terms, these remain the same so this generic implementation does nothing.
Definition at line 239 of file symbolic.hpp.
◆ simplify() [1/13]
| void sym::simplify | ( | ) |
By default, there is no generic simplify implemented. There should be a compiler error if no simplify is available.
◆ simplify() [2/13]
| auto sym::simplify | ( | const PowerOp< Arg, C< Power, 1 > > & | f | ) | -> STATOR_AUTORETURN(simplify_powerop_impl<Config>(f, detail::select_overload |
This implementation only works if the argument has an simplify function defined for its argument.
Definition at line 210 of file simplify.hpp.
◆ simplify() [3/13]
| auto sym::simplify | ( | BinaryOp< L, Op, R > | t | ) | -> STATOR_AUTORETURN(simplify_BinaryOp<Config>(t, detail::select_overload |
Definition at line 251 of file simplify.hpp.
◆ simplify() [4/13]
| Polynomial<Order+1, Real, typename variable_combine<PolyVar, Var<VarArgs...> >::type> sym::simplify | ( | const MultiplyOp< Polynomial< Order, Real, PolyVar >, Var< VarArgs... > > & | f | ) |
Definition at line 279 of file simplify.hpp.
◆ simplify() [5/13]
| auto sym::simplify | ( | Var< VarArgs... > | ) | -> STATOR_AUTORETURN((Polynomial<1, int, Var<VarArgs...> > |
Definition at line 290 of file simplify.hpp.
◆ simplify() [6/13]
| Polynomial<Power, int, Var<VarArgs...> > sym::simplify | ( | const PowerOp< Var< VarArgs... >, C< Power, 1 > > & | ) |
Definition at line 297 of file simplify.hpp.
◆ simplify() [7/13]
| auto sym::simplify | ( | const C< num, den > & | f | ) | -> STATOR_AUTORETURN(typename Config::expand_Constants_to_t(num)/typename Config::expand_Constants_to_t(den)) |
◆ simplify() [8/13]
| auto sym::simplify | ( | const BinaryOp< Polynomial< N, Real1, PolyVar1 >, Op, Polynomial< M, Real2, PolyVar2 >> & | f | ) | -> Polynomial<detail::max_order(M, N), decltype(store(Op::apply(f._l[0],f._r[0]))), typename variable_combine<PolyVar1, PolyVar2>::type> |
Definition at line 349 of file simplify.hpp.
◆ simplify() [9/13]
| auto sym::simplify | ( | const BinaryOp< Polynomial< M, Real1, PolyVar1 >, Op, Polynomial< N, Real2, PolyVar2 >> & | f | ) | -> Polynomial<M + N, decltype(store(Op::apply(f._l[0], f._r[0]))), typename variable_combine<PolyVar1, PolyVar2>::type> |
Definition at line 371 of file simplify.hpp.
◆ simplify() [10/13]
| auto sym::simplify | ( | const BinaryOp< Polynomial< M, Real1, PolyVar1 >, detail::Divide, Polynomial< 0, Real2, PolyVar2 >> & | f | ) | -> Polynomial<M, decltype(store(f._l[0] / f._r[0])), typename variable_combine<PolyVar1, PolyVar2>::type> |
Definition at line 384 of file simplify.hpp.
◆ simplify() [11/13]
| auto sym::simplify | ( | const UnaryOp< Arg, Op > & | f | ) | -> STATOR_AUTORETURN(simplify_UnaryOp<Config>(f, detail::select_overload |
Definition at line 430 of file simplify.hpp.
◆ simplify() [12/13]
| auto sym::simplify | ( | const PowerOp< UnaryOp< Arg, detail::Arbsign >, C< Power, 1 > > & | f | ) | -> typename std::enable_if<!(Power % 2), decltype(try_simplify<Config>(pow(f._l._arg, C<Power>())))>::type |
Definition at line 454 of file simplify.hpp.
◆ simplify() [13/13]
Definition at line 511 of file runtime.hpp.
◆ simplify_BinaryOp() [1/21]
| auto sym::simplify_BinaryOp | ( | const BinaryOp< LHS, Op, RHS > & | f, |
| detail::choice< 0 > | |||
| ) | -> typename std::enable_if<!std::is_same<decltype(Op::apply(f._l, f._r)), BinaryOp<LHS, Op, RHS> >::value, decltype(Op::apply(f._l, f._r))>::type |
Definition at line 128 of file simplify.hpp.
◆ simplify_BinaryOp() [2/21]
| Op::right_zero sym::simplify_BinaryOp | ( | const BinaryOp< LHS, Op, RHS > & | , |
| detail::choice< 0 > | |||
| ) |
Definition at line 135 of file simplify.hpp.
◆ simplify_BinaryOp() [3/21]
| Op::left_zero sym::simplify_BinaryOp | ( | const BinaryOp< LHS, Op, RHS > & | , |
| detail::choice< 0 > | |||
| ) |
Definition at line 139 of file simplify.hpp.
◆ simplify_BinaryOp() [4/21]
| auto sym::simplify_BinaryOp | ( | const BinaryOp< LHS, Op, typename Op::right_identity > & | op, |
| detail::choice< 0 > | |||
| ) | -> STATOR_AUTORETURN(try_simplify< Config >(op._l)) |
◆ simplify_BinaryOp() [5/21]
| auto sym::simplify_BinaryOp | ( | const BinaryOp< typename Op::left_identity, Op, RHS > & | op, |
| detail::choice< 0 > | |||
| ) | -> STATOR_AUTORETURN(try_simplify< Config >(op._r)) |
◆ simplify_BinaryOp() [6/21]
| Unity sym::simplify_BinaryOp | ( | const BinaryOp< Var< VarArgs1... >, detail::Divide, Var< VarArgs2... >> & | op, |
| detail::choice< 0 > | |||
| ) |
Definition at line 152 of file simplify.hpp.
◆ simplify_BinaryOp() [7/21]
| RHS sym::simplify_BinaryOp | ( | const SubtractOp< Null, RHS > & | r, |
| detail::choice< 0 > | |||
| ) |
Definition at line 157 of file simplify.hpp.
◆ simplify_BinaryOp() [8/21]
| auto sym::simplify_BinaryOp | ( | const MultiplyOp< Var< VarArgs1... >, Var< VarArgs2... > > & | , |
| detail::choice< 0 > | |||
| ) | -> STATOR_AUTORETURN(sym::pow(typename variable_combine< Var< VarArgs1... >, Var< VarArgs2... > >::type(), C< 2 >())) |
◆ simplify_BinaryOp() [9/21]
| auto sym::simplify_BinaryOp | ( | const MultiplyOp< PowerOp< Var< VarArgs1... >, Order >, Var< VarArgs2... > > & | f, |
| detail::choice< 0 > | |||
| ) | -> STATOR_AUTORETURN(sym::pow(typename variable_combine<Var<VarArgs1...>, Var<VarArgs2...> >::type |
Definition at line 167 of file simplify.hpp.
◆ simplify_BinaryOp() [10/21]
| auto sym::simplify_BinaryOp | ( | const MultiplyOp< Var< VarArgs1... >, PowerOp< Var< VarArgs2... >, Order > > & | f, |
| detail::choice< 0 > | |||
| ) | -> STATOR_AUTORETURN(sym::pow(typename variable_combine<Var<VarArgs1...>, Var<VarArgs2...> >::type |
Definition at line 172 of file simplify.hpp.
◆ simplify_BinaryOp() [11/21]
| auto sym::simplify_BinaryOp | ( | const BinaryOp< LHS, Op, RHS > & | f, |
| detail::choice< 2 > | |||
| ) | -> STATOR_AUTORETURN(try_simplify< Config >(Op::apply(simplify< Config >(f._l), simplify< Config >(f._r)))) |
◆ simplify_BinaryOp() [12/21]
| auto sym::simplify_BinaryOp | ( | const BinaryOp< LHS, Op, RHS > & | f, |
| detail::choice< 3 > | |||
| ) | -> STATOR_AUTORETURN(try_simplify< Config >(Op::apply(simplify< Config >(f._l), f._r))) |
◆ simplify_BinaryOp() [13/21]
| auto sym::simplify_BinaryOp | ( | const BinaryOp< BinaryOp< Arg1, Op, Arg2 >, Op, Arg3 > & | f, |
| detail::choice< 6 > | |||
| ) | -> STATOR_AUTORETURN(try_simplify< Config >(Op::apply(f._l._l, simplify< Config >(BinaryOp< Arg2, Op, Arg3 >(f._l._r, f._r))))) |
◆ simplify_BinaryOp() [14/21]
| auto sym::simplify_BinaryOp | ( | const BinaryOp< Arg1, Op, BinaryOp< Arg2, Op, Arg3 > > & | f, |
| detail::choice< 6 > | |||
| ) | -> STATOR_AUTORETURN(try_simplify< Config >(Op::apply(simplify< Config >(BinaryOp< Arg1, Op, Arg2 >(f._l, f._r._l)), f._r._r))) |
◆ simplify_BinaryOp() [15/21]
| auto sym::simplify_BinaryOp | ( | const BinaryOp< BinaryOp< Arg1, Op, Arg2 >, Op, Arg3 > & | f, |
| detail::choice< 7 > | |||
| ) | -> STATOR_AUTORETURN(try_simplify< Config >(Op::apply(simplify< Config >(BinaryOp< Arg1, Op, Arg3 >(f._l._l, f._r)), f._l._r))) |
◆ simplify_BinaryOp() [16/21]
| auto sym::simplify_BinaryOp | ( | const BinaryOp< Arg1, Op, BinaryOp< Arg2, Op, Arg3 > > & | f, |
| detail::choice< 7 > | |||
| ) | -> STATOR_AUTORETURN(try_simplify< Config >(Op::apply(simplify< Config >(BinaryOp< Arg1, Op, Arg3 >(f._l, f._r._r)), f._r._l))) |
◆ simplify_BinaryOp() [17/21]
| auto sym::simplify_BinaryOp | ( | const BinaryOp< Polynomial< Order, Real, PolyVar >, Op, Real2 > & | f, |
| detail::last_choice | |||
| ) | -> STATOR_AUTORETURN(try_simplify<Config>(Op::apply(f._l, Polynomial<0, decltype(toArithmetic(f._r)), PolyVar> |
Definition at line 329 of file simplify.hpp.
◆ simplify_BinaryOp() [18/21]
| auto sym::simplify_BinaryOp | ( | const BinaryOp< Real2, Op, Polynomial< Order, Real, PolyVar >> & | f, |
| detail::last_choice | |||
| ) | -> STATOR_AUTORETURN(try_simplify<Config>(Op::apply(Polynomial<0, decltype(toArithmetic(f._l)), PolyVar> |
Definition at line 336 of file simplify.hpp.
◆ simplify_BinaryOp() [19/21]
| auto sym::simplify_BinaryOp | ( | const BinaryOp< UnaryOp< Arg1, detail::Arbsign >, Op, UnaryOp< Arg2, detail::Arbsign > > & | f, |
| detail::choice< 4 > | |||
| ) | -> STATOR_AUTORETURN(try_simplify< Config >(detail::Arbsign::apply(Op::apply(f._l._arg, f._r._arg)))) |
◆ simplify_BinaryOp() [20/21]
| auto sym::simplify_BinaryOp | ( | const BinaryOp< LHS, Op, UnaryOp< Arg, detail::Arbsign > > & | f, |
| detail::choice< 5 > | |||
| ) | -> STATOR_AUTORETURN(try_simplify< Config >(detail::Arbsign::apply(Op::apply(f._l, f._r._arg)))) |
◆ simplify_BinaryOp() [21/21]
| auto sym::simplify_BinaryOp | ( | const BinaryOp< UnaryOp< Arg, detail::Arbsign >, Op, RHS > & | f, |
| detail::choice< 5 > | |||
| ) | -> STATOR_AUTORETURN(try_simplify< Config >(detail::Arbsign::apply(Op::apply(f._l._arg, f._r)))) |
◆ simplify_powerop_impl() [1/2]
| auto sym::simplify_powerop_impl | ( | const PowerOp< Arg, C< Power, 1 > > & | f, |
| detail::choice< 0 > | |||
| ) | -> STATOR_AUTORETURN(try_simplify< Config >(PowerOpSub< Power >::eval(simplify< Config >(f._l)))) |
◆ simplify_powerop_impl() [2/2]
| auto sym::simplify_powerop_impl | ( | const PowerOp< Arg, C< Power, 1 > > & | f, |
| detail::choice< 1 > | |||
| ) | -> STATOR_AUTORETURN(simplify< Config >(PowerOpSub< Power >::eval(f._l))) |
◆ simplify_UnaryOp() [1/2]
| auto sym::simplify_UnaryOp | ( | const UnaryOp< UnaryOp< Arg, detail::Arbsign >, detail::Arbsign > & | f, |
| detail::choice< 0 > | |||
| ) | -> STATOR_AUTORETURN(try_simplify< Config >(detail::Arbsign::apply(f._arg._arg))) |
Division of a Polynomial by a constant.
◆ simplify_UnaryOp() [2/2]
| auto sym::simplify_UnaryOp | ( | const UnaryOp< Arg, Op > & | f, |
| detail::last_choice | |||
| ) | -> STATOR_AUTORETURN(try_simplify< Config >(Op::apply(simplify< Config >(f._arg)))) |
◆ sin() [1/6]
|
inline |
Definition at line 35 of file unary_ops.hpp.
◆ sin() [2/6]
|
inline |
Definition at line 36 of file unary_ops.hpp.
◆ sin() [3/6]
|
inline |
Definition at line 37 of file unary_ops.hpp.
◆ sin() [4/6]
| std::complex<T> sym::sin | ( | std::complex< T > | a | ) |
Definition at line 38 of file unary_ops.hpp.
◆ sin() [5/6]
| auto sym::sin | ( | const Arg & | arg | ) | -> STATOR_AUTORETURN((UnaryOp< decltype(store(arg)), detail::Sine >(arg))) |
◆ sin() [6/6]
| auto sym::sin | ( | const C< num, den > & | a | ) | -> STATOR_AUTORETURN(sin_Cimpl(a, detail::select_overload |
Definition at line 183 of file constants.hpp.
◆ sin_Cimpl() [1/2]
| constexpr Null sym::sin_Cimpl | ( | const C< num, den > & | a, |
| detail::choice< 0 > | |||
| ) |
Definition at line 168 of file constants.hpp.
◆ sin_Cimpl() [2/2]
| constexpr Unity sym::sin_Cimpl | ( | const C< num, den > & | a, |
| detail::choice< 0 > | |||
| ) |
Definition at line 172 of file constants.hpp.
◆ solve_real_roots()
|
inline |
Definition at line 217 of file symbolic.hpp.
◆ sub() [1/6]
| auto sym::sub | ( | BinaryOp< LHS, Op, RHS > | f, |
| Relation< Var, Arg > | x | ||
| ) | -> STATOR_AUTORETURN_BYVALUE(Op::apply(sub(f._l, x), sub(f._r, x))) |
◆ sub() [2/6]
| auto sym::sub | ( | const UnaryOp< Arg1, Op > & | f, |
| const Relation< Var, Arg2 > & | x | ||
| ) | -> STATOR_AUTORETURN(Op::apply(sub(f._arg, x))) |
◆ sub() [3/6]
| auto sym::sub | ( | const T & | f, |
| const Relation< Var, Arg > & | |||
| ) | -> STATOR_AUTORETURN_BYVALUE(f) |
This implementation only applies if the term is a constant term.
We deliberately return by const reference as, if this is an Eigen expression, the Eigen library may take an internal reference to this object to allow delayed evaluation. By returning the original object we can try to ensure its lifetime is at least longer than the current expression.
◆ sub() [4/6]
| auto sym::sub | ( | const Var< Args1... > & | f, |
| const Relation< Var< Args2... >, Arg > & | x | ||
| ) | -> STATOR_AUTORETURN_BYVALUE(x._val) |
This is only used if the Var is correct substitution.
◆ sub() [5/6]
| Var<Args1...> sym::sub | ( | const Var< Args1... > & | f, |
| const Relation< Var2, Arg > & | x | ||
| ) |
This is only used if the Var is not the correct letter for the substitution.
Definition at line 193 of file symbolic.hpp.
◆ sub() [6/6]
Definition at line 556 of file runtime.hpp.
◆ subtraction_precision()
| size_t sym::subtraction_precision | ( | const T | f1, |
| const T | f2 | ||
| ) |
If two floats are being subtracted, the precision of the operation is related to how close the numbers are. If they are of the same magnitude the precision may be terrible (so called catastrophic cancellation). We can rank how precise the operation is by comparing the difference in their exponents. A larger difference is always better, so the absolute difference is returned by this function.
This function also handles the special cases where one or more of the arguments.
Definition at line 47 of file precision.hpp.
◆ taylor_series()
| auto sym::taylor_series | ( | const F & | f, |
| Real | a, | ||
| Var | |||
| ) | -> STATOR_AUTORETURN(try_simplify(detail::TaylorSeriesWorker< 0, Order, Var >::eval(f, a))) |
◆ toArithmetic() [1/4]
| auto sym::toArithmetic | ( | T | val | ) | -> STATOR_AUTORETURN_BYVALUE(val) |
◆ toArithmetic() [2/4]
| auto sym::toArithmetic | ( | std::complex< T > | val | ) | -> STATOR_AUTORETURN_BYVALUE(val) |
◆ toArithmetic() [3/4]
| std::intmax_t sym::toArithmetic | ( | C< n1, d1 > | val | ) |
Definition at line 315 of file simplify.hpp.
◆ toArithmetic() [4/4]
| double sym::toArithmetic | ( | C< n1, d1 > | val | ) |
Definition at line 319 of file simplify.hpp.
◆ try_expand()
| auto sym::try_expand | ( | const T & | a | ) | -> STATOR_AUTORETURN(try_simplify< ExpandConfig >(a)) |
◆ try_N()
| auto sym::try_N | ( | const T & | a | ) | -> STATOR_AUTORETURN(try_simplify< NConfig >(a)) |
◆ try_simplify()
| auto sym::try_simplify | ( | const T & | a | ) | -> decltype(detail::try_simplify_imp<Config>(a, detail::select_overload |
Definition at line 84 of file simplify.hpp.
Variable Documentation
◆ _r
| f sym::_r |
Definition at line 337 of file simplify.hpp.
 1.8.13
1.8.13