This is a short introduction to the compile-time symbolic algebra library (see symbolic_example.cpp).

To use stator, first include the stator::sym library header file and bring the sym namespace into scope for convenience:

#include <stator/symbolic/symbolic.hpp>
int main(int argc, char **argv) {
  using namespace sym;

Variables

Variables are a critical component of a CAS system. Each variable is a placeholder for a future expression and thus needs a unique index to identify it. These are identified in stator either using a single character or an index:

  //The default variable is the letter x
  Var<> x;
  
  //But you can specify your own variables by letter:
  Var<vidx<'y'> > y;
  
  //Or by index:
  Var<vidx<42>> v42;

Expressions using variables (and all derived classes of sym::SymbolicOperator) are not evaluated immediately, but result in symbolic expressions:

  //We have to catch symbolic expressions using "auto" as their type is very complex
  auto f1 = x * x + sin(y);
  
  std::cout << f1 << std::endl;
  //Output: ((x × x) + sin(y))

Variables can be substituted for other variables, for example, we can replace 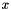$x$ with $y+2$ :

  auto f1_xsub = sub(f1, x = y + 2);
  
  std::cout << f1_xsub << std::endl;
  //Output: (((y + 2) × (y + 2)) + sin(y))

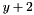To evaluate an expression, all variables (and other symbolic types) must be substituted for non-symbolic values. A final substitution for 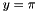$y=\pi$ in the previous expression causes a complete evaluation to a double type:

std::cout << sub(f1_xsub, y = 3.14159265359) << std::endl;

//Output: 26.436...

All of this is evaluated at compile time into the basic floating point operations, which also may be optimised away, thus complex mathematics may be written in a natural way without worrying about computational cost.

Rational constants

Stator can work with standard arithmetic terms (integers, floats); however, they only have limited compile-time symbolic support. For example, the following expression cannot be simplified by stator:

  auto f2 = (3-3) * x;
  std::cout << f2 << std::endl;
  //Output: (0 × x)

The difficulty here is that the compiler cannot deduce the value of an integer or float from its type (which is all the compiler has access to). C++11 gave us std::ratio, which allows rational constants to be encoded as a ratio of two integer values. In stator, this has been extended to give the rational constant type, sym::C. This allows the compiler to perform rational arithmetic at compile time:

  C<1, 2> half;
  C<2> two;
  
  //Compile-time rational arithmetic!
  auto three = half + half + two;
  //The variable three is of type "C<3>", thus it must be computed at compile time.
  assert((std::is_same<decltype(three), C<3> >::value)); //does not fail
  
  std::cout << three << std::endl;
  //Output: C<3>()

When the rational constant type sym::C is used, stator can cancel zero terms. For example, any term multiplied by C<0> (which has a convenient typedef of sym::Null) is cancelled to zero at compile time:

  auto f3 = (C<1>() - C<1>()) * sin(x);
  std::cout << f3 << std::endl;
  //Output: C<0>()

Equally, any term multiplied by C<1> (which has a convenient typedef of sym::Unity), is left unchanged:

  auto f4 = C<1>() * sin(x);
  std::cout << f4 << std::endl;
  //Output: sin(x)

To enable this powerful simplification, sym::C values should be used wherever possible.

Calculus, simplification, and other transformations

As mathematical expressions are encoded as types, the compiler can apply transformations to them. For example, the derivative can be evaluated at compile-time:

  auto f5 = cos(2 * x);
  auto df5_dx = derivative(f5, x);
  std::cout << df5_dx << std::endl;
  //Output: (-2 × sin((2 × x)))

More complex operations are available, such as Taylor series:

  //A taylor series of sin(2x) around zero
  std::cout << taylor_series<3>(sin(C<2>() * x), C<0>(), x) << std::endl;
  //Output: (x × (C<2>() + ((x ^ C<2>()) × C<-4,3>())))

The output can rapidly become ugly. Fortunately, basic simplification is available via sym::simplify. For example:

  std::cout << x * x * x * x * x << std::endl;
  //Output: ((((x × x) × x) × x) × x)
  std::cout << simplify(x * x * x * x * x) << std::endl;
  //Output: (x ^ C<5>())         (which is equivalent to "pow(x, C<5>())")

Please note, simplify only exists if there is a simplification to be made and will fail at compile time if there is not. You can also use sym::try_simplify if you do not want missing simplification to be an error.

The Taylor series expansion above actually has no simplification. However, it can be converted into a Polynomial type, which gives a simpler representation and allows further functional analysis.

Polynomial types

The sym::expand function attempts to collect the coefficients of a polynomial and create a sym::Polynomial type:

  
  auto f6 = taylor_series<3>(sin(C<2>() * x), C<0>(), x);
  std::cout << f6 << std::endl;
  //Output: (x × (C<2>() + ((x ^ C<2>()) × C<-4,3>())))
  auto f6_poly = expand(f6);
  std::cout << f6_poly << std::endl;
  //Output: P(-1.33333 × x³ + 2 × x)

The output here is a sym::Polynomial type (as indicated by the "P()" wrapper). The sym::Polynomial is simply an array of coefficients, from lowest to highest order:

  std::cout << f6_poly[0] << std::endl;
  //Output: 0
  std::cout << f6_poly[3] << std::endl;
  //Output: -1.33333

Most importantly, the polynomial type allows further functional analysis, such as determining the roots of the polynomial:

  //Then we can analyse its real roots!
  auto f6_roots = solve_real_roots(f6_poly);
  std::cout << f6_roots << std::endl;
  //Output: StackVector{ -1.22474 0 1.22474 }
  //Extracting the number of roots
  std::cout << f6_roots.size() << std::endl;
  //Output: 3
  
  //Extracting a value of a root
  std::cout << f6_roots[2] << std::endl;
  //Output: 1.22474

Here there are three real roots, and they are returned in a StackVector, which is like a std::vector with a fixed maximum size allowing it to be allocated on the stack.

The library is capable of solving for all of the real roots of arbitrary polynomials but relies on numerical iteration schemes for polynomials of any order greater than three.

Vector expressions

The symbolic library also supports Eigen vector/matrix expressions.

  Eigen::Matrix<double, 1, 3> r{1.0, 2.0, 3.0};
  Eigen::Matrix<double, 1, 3> v{1.0, 0.5, 0.1};
  auto fvec = r + x * v;
  std::cout << sub(fvec, x = 12) << std::endl;
  //Output:  13   8 4.2

You have to be careful though. Eigen preserves the row/column nature of the vectors so operations like multiplication may cause compile errors